In this assignment, you will write code to compute an optimal policy for a given MDP using the algorithms that were discussed in class: Value Iteration, Howard's Policy Iteration, and Linear Programming. The first part of the assignment is to implement these algorithms. Input to these algorithms will be an MDP and the expected output is the optimal value function, along with an optimal policy.

MDP solvers have a variety of applications. As the second part of this assignment, you will use your solver to find an optimal policy for each player in the game of Anti-Tic-Tac-Toe, which is a variant of Tic-Tac-Toe that we have created specifically for this assignment.

This compressed directory (updated 4.00 p.m. September 28) contains a data directory with sample data for both parts and helper functions to visualize and test your code. Your code will also be evaluated on instances other than the ones provided.

Part 1: MDP Planning

Data

In the mdp folder in data directory, you are given six MDP instances (3 each for continuing and episodic tasks). A correct solution for each MDP is also given in the same folder, which you can use to test your code.

MDP file format

Each MDP is provided as a text file in the following format.

The number of states S and the number of actions A will be integers greater than 1. There will be at most 2500 states, and at most 100 actions. Assume that the states are numbered 0, 1, ..., S - 1, and the actions are numbered 0, 1, ..., A - 1. Each line that begins with "transition" gives the reward and transition probability corresponding to a transition, where R(s1, ac, s2) = r and T(s1, ac, s2) = p. Rewards can be positive, negative, or zero. Transitions with zero probabilities are not specified. mdptype will be one of continuing and episodic. The discount factor gamma is a real number between 0 (included) and 1 (included). Recall that gamma is a part of the MDP: you must not change it inside your solver! Also recall that it is okay to use gamma = 1 in episodic tasks that guarantee termination; you will find such an example among the ones given.

To get familiar with the MDP file format, you can view and run generateMDP.py (provided in the base directory), which is a python script used to generate random MDPs. Specify the number of states and actions, the discount factor, type of MDP (episodic or continuing), and the random seed as command-line arguments to this file. Two examples of how this script can be invoked are given below.

• python generateMDP.py --S 2 --A 2 --gamma 0.90 --mdptype episodic --rseed 0
• python generateMDP.py --S 50 --A 20 --gamma 0.20 --mdptype continuing --rseed 0

Task 1 - MDP Planning Algorithms

Given an MDP, your program must compute the optimal value function V* and an optimal policy π* by applying the algorithm that is specified through the command line. Create a python file called planner.py which accepts the following command-line arguments.

• --mdp followed by a path to the input MDP file, and
• --algorithm followed by one of vi, hpi, and lp.

Make no assumptions about the location of the MDP file relative to the current working directory; read it in from the path that will be provided. The algorithms specified above correspond to Value Iteration, Howard's Policy Iteration, and Linear Programming, respectively. Here are a few examples of how your planner might be invoked (it will always be invoked from its own directory).

• python planner.py --mdp /home/user/data/mdp-4.txt --algorithm vi
• python planner.py --mdp /home/user/temp/data/mdp-7.txt --algorithm hpi
• python planner.py --mdp /home/user/mdpfiles/mdp-5.txt --algorithm lp
• python planner.py --mdp /home/user/mdpfiles/mdp-5.txt

Notice that the last call does not specify which algorithm to use. If this is the case, your code must have a default algorithm from vi, hpi, and lp that gets called. This feature will come handy when your planner is used in Task 2. It gives you the flexibility to use whichever algorithm you prefer.

You are not expected to code up a solver for LP; rather, you can use available solvers as black-boxes (more below). Your effort will be in providing the LP solver the appropriate input based on the MDP, and interpreting its output appropriately. Use the formulation presented in class. You are expected to write your own code for Value Iteration and Howard's Policy Iteration; you may not use any custom-built libraries that might be available for the purpose. You can use libraries for solving linear equations in the policy evaluation step but must write your own code for policy improvement. Recall that Howard's Policy Iteration switches all improvable states to some improving action; if there are two or more improving actions at a state, you are free to pick anyone.

It is certain that you will face some choices while implementing your algorithms, such as in tie-breaking, handling terminal states, and so on. You are free to resolve in any reasonable way; just make sure to note your approach in your report.

Output Format

The output of your planner must be in the following format and written to standard output.

  V*(0)   π*(0)
  V*(1)   π*(1)
  .
  .
  .
  V*(S - 1)   π*(S - 1)
  

In the data/mdp directory provided, you will find output files corresponding to the MDP files, which have solutions in the format above.

Since your output will be checked automatically, make sure you have nothing printed to stdout other than the S lines as above in sequence. If the testing code is unable to parse your output, you will not receive any marks.

Note:

1. Your output has to be written to the standard output, not to any file.
2. For values, print at least 6 places after the decimal point. Print more if you'd like, but 6 (xxx.123456) will suffice.
3. If your code produces output that resembles the solution files: that is, S lines of the form

   value + "\t" + action + "\n"
             

   or even

   value + " " + action + "\n"
             

   you should be okay. Make sure you don't print anything else.

4. If there are multiple optimal policies, feel free to print any one of them.

You are given a python script to verify the correctness of your submission format and solution: PlannerVerifyOutput.py. The following are a few examples that can help you understand how to invoke this script.

• python PlannerVerifyOutput.py --> Tests the default algorithm set in planner.py on the all the MDP instances given to you in the data/mdp directory.
• python PlannerVerifyOutput.py --algorithm all --> Tests all three algorithms + default algorithm on the all the MDP instances give to you in the data/mdp directory.
• python PlannerVerifyOutput.py --algorithm vi --> Tests only value iteration algorithm on the all the MDP instances given to you in the data/mdp directory.

The script assumes the location of the data directory to be in the same directory. Run the script to check the correctness of your submission format. Your code should pass all the checks written in the script. You will be penalised if your code does not pass all the checks.

Your code for any of the algorithms should not take more than one minute to run on any test instance.

Part 2: Anti-Tic-Tac-Toe Game

The Game

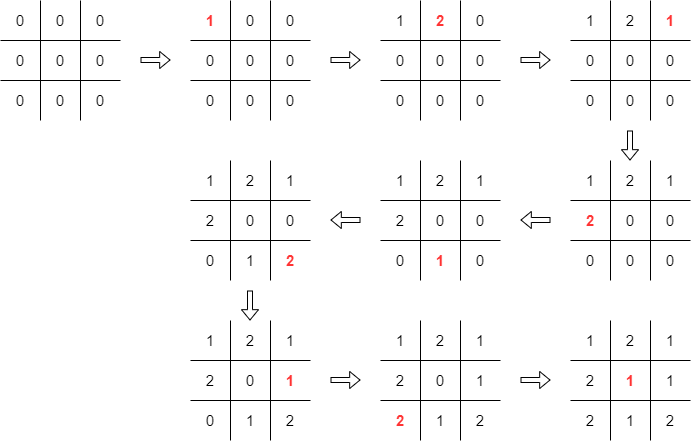
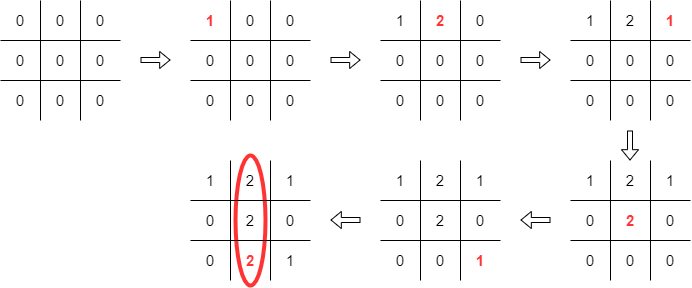
We define the rules of Anti-Tic-Tac-Toe to be identical to those of conventional Tic-Tac-Toe, with the twist that the winning conditions are reversed. The game is played between Player 1 and Player 2 on a 3x3 grid that is initially empty. Player 1 plays the first move by claiming one of the cells; Player 2 plays the next move, claiming one of the empty cells; the players alternate in this fashion until a terminal state is reached.

If a state has an entire row, column, or diagonal filled by a particular player, it is a terminal state. A state with all nine cells filled is also a terminal state. If the game ends in a terminal state in which Player 1 (2) has a fully-filled row, column, or diagonal, then Player 2 (1) is the winner (this is the difference with regular Tic-Tac-Toe). If termination is on account of the board becoming fully filled with no completed row, column, or diagonal, the result is a draw.

Below are traces from two Anti-Tic-Tac-Toe games that help visualise the progress of the game. We adopt the convention of putting a "0" entry in empty cells.

Data

Although an initial estimate would suggest there are 3⁹ possible states in Anti-Tac-Tac-Toe, a close look rules out many of these "states" from being reached. Moreover, each player has a separate set of states from which it can make its moves. In the attt folder of the data directory, you are given 2 files within the states directory, each listing the set of possible states from which each player can make moves. The sequence in which these states are given is important: you must retain the same sequence when your code for Anti-Tic-Tac-Toe interfaces with your MDP planner.

You will also find a policies folder within data/attt, which provides examples of policies (assumed to be stochastic) of players 1 and 2. Below we give more detailed technical specifications.

State Representation

• 0 Indicates the given cell is blank.
• 1 Indicates Player 1 has filled the cell.
• 2 Indicates Player 2 has filled the cell.

State File Format

You are provided with two state files, each of which lists the valid states that can be encountered by Player 1 and Player 2. A valid state for a given player is a state in which that player can play a move. For example, 102012102 is a terminal state (which results in a win for Player 1). It is not valid for either player. 101202100 is valid for Player 2, but not for Player 1. For illustration, below we have pasted the first few lines from the state file for player 1.

Policy File Format

A policy specifies the complete behaviour of any one of the players. In policy files, the index of the player whose behaviour is being fixed is given in the very first line. Subsequent lines all have 10 entries: the first specifying the state, and the subsequent entries giving the probabilities of taking actions 1 through 9. Taking action i means filling up cell i in the flattened grid. In the files we have given you, illegal actions (attempting to fill a cell that is already filled) all have zero probability. Naturally, the policies you compute must also satisfy this constraint (else they will be invalid).

The snippet below corresponds to a policy of Player 1.

1
000000000   0.11111   0.11111   0.11111   0.11111   0.11111   0.11111   0.11111   0.11111   0.11111
120000000   0.00000   0.00000   0.14285   0.14285   0.14285   0.14285   0.14285   0.14285   0.14285
121200000   0.00000   0.00000   0.00000   0.00000   0.20000   0.20000   0.20000   0.20000   0.20000
121212000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.33333   0.33333   0.33333
121212210   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   1.00000
121212012   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   1.00000   0.00000   0.00000
121210200   0.00000   0.00000   0.00000   0.00000   0.00000   0.33333   0.00000   0.33333   0.33333
121211220   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   1.00000
121211202   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   1.00000   0.00000
. . .
. . .
. . .

Task 2 - MDP for Anti-Tic-Tac-Toe Game

In this task, your objective is to find an optimal policy for a player with respect to a fixed opponent's policy, in the game of Anti-Tic-Tac-Toe. Assume that a win earns a score of 1, every other outcome (draw, loss) earns 0. An optimal player (against a fixed opponent) maximises their expected score against that opponent from every valid state as start state, which is equivalent to maximising the win probability from every valid state as start state. (In principle we can distinguish draws from losses, but for simplicity we choose not to.)

Rather than write a solver from scratch, all you need to do is to translate the above task into an MDP, and use the solver you have already created in Task 1.

Your first step is to write an encoder script which takes as input the opponent's policy and encodes the game into an MDP (use the same format as described above). So, for example, if the input policy gives the behaviour of Player 2, you must create an MDP in which Player 1 is the agent, and Player 2's actions get folded into the environment. In particular, note that whenever Player 1 makes a move, its next state can be determined only by considering the subsequent move of Player 2 (unless a terminal state is reached before that happens).

Your next step is to take the output of the encoder script and use it as input to planner.py. As usual, planner.py will provide as output an optimal policy and value function.

Finally, create a python file called decoder.py that will take the output from planner.py and convert it into a policy file, having the same format as stated above. Thus, the sequence of encoding, planning, and decoding results in the computation of an optimal policy for a player given a fixed policy of the other player.

Here is the sequence of instructions that we will execute to obtain your optimal counter-policy.

If the policy file that you intend to provide as input to the encoder corresponds to Player 1 (2), then the state file path must correspond to the state file for Player 2 (1); the player ID and states file passed to the decoder will be that of Player 2 (1).

As stated earlier, note that the planner must use its default algorithm. You can use AtttVerifyOutput.py to verify that your encoding and decoding scripts produce output in the correct format. Here is how you would use it.

The eventual output policyfile will be evaluated by us (using our own code) to check if it achieves optimal score from every valid state.

To help you build intuition and debug as you develop your Anti-Tic-Tac-Toe player, we give you a command line based interactive UI for playing the game: attt.py. The script allows you to play yourself (for one or both of the players), else fix one or both to play according to a given policy. You are free to change the random seed, too (in the code itself).

• python attt.py --> For playing a normal 2 player game.
• python attt.py -p1 player1_policyfile --> For playing against a Player 1 opponent with a given policy.
• python attt.py -p1 player1_policyfile -p2 player2_policyfile --> For automating a game between two players with the respective policies.

Task 3 - Anti-Tic-Tac-Toe Optimal Strategy

In Task 2, you used your MDP planner to solve for an optimal policy against any fixed opponent in Anti-Tic-Tac-Toe. But what would you do if you are not told which opponent you are playing against? This question has received a lot of attention from game theory; if time permits, we might be able to have a lecture on multi-agent learning as a part of this course (even if the current question is one of planning, rather than learning). For now, you are asked to implement an intuitive approach for trying to realise progressively "better" players. Suppose we initialise Player 2 with some arbitrary policy π[0]. Let π[1] be an optimal policy for Player 1 against π[0]. You can use your planner from Task 2 to compute π[1]. Now again, let π[2] be an optimal policy for Player 2 against π[1], and π[3] an optimal policy for Player 1 against π[2]. You get the idea: starting with an initial policy, we keep computing optimal counter-policies for the latest policies, resulting in even-numbered policies for Player 2, and odd-numbered policies for Player 1. Of course, you could also have started with an initial policy for Player 1, and implemented the same scheme to generate sequences of policies for Player 2 and Player 1. When you freeze the policy for Player A, and optimise Player B, note that Player B seeks to maximise its expected score. Hence, there is no need for you to negate rewards depending on the player index.

In this task, you must implement the "outer loop" described above to generate sequences of policies for Player 1 and Player 2. You are free to experiment with different initial policies and different players being initially fixed. It would be a good idea to generate at least 10 policies for each player from the starting point. Write a script called task3.py in order to do so. To generate each pair, the script must use the encode-plan-decode sequence of operations from Task 2. Make sure task3.py does not take any command line arguments; if needed you can hard-code random seeds or initial policies internally.

Although we don't have a rigid definition of what your script must do, you must use it to monitor the policies generated, so that the empirical behaviour observed helps you answer the following question.

Question: Is the sequence of policies generated for each player guaranteed to converge? If yes, provide a proof of convergence, and describe the properties of the converged policy. If not, either give a concrete counter-example, or qualitative arguments for why the process could go on for ever. If your answer depends on implementational aspects such as tie-breaking, be sure to specify your assumptions.

We will evaluate your subjective answer to the question above. As a part of your question, refer to the data you have generated using task3.py. For example, the code could print out whether each pair of successive policies from the sequences 0, 2, 4, ... and 1, 3, 5, ... differ or not for a few initialisations. The empirical pattern ought to be explained by the accompanying proof. You can keep your proof relatively high-level and informal; no need to adopt heavy mathematical language.

Submission

Prepare a short report.pdf file, in which you put your design decisions, assumptions, and observations about the algorithms (if any) for Task 1. Also describe how you formulated the MDP for the Anti-Tic-Tac-Toe problem: that is, for Task 2. Your answer to Task 3 must also be placed in this same report. If you'd like, you can include snippets of the output of task3.py; otherwise you can refer to the output, which we will generate by running the same script.

Place all the files in which you have written code in a directory named submission. Tar and Gzip the directory to produce a single compressed file (submission.tar.gz). It must contain the following files.

1. planner.py
2. encoder.py
3. decoder.py
4. task3.py
5. report.pdf
6. references.txt
7. Any other files required to run your source code

Submit this compressed file on Moodle, under Programming Assignment 2.

Evaluation

8 marks are reserved for Task 1 (2 marks for the correctness of your Value Iteration algorithm, and 3 marks each for Howard's Policy Iteration and Linear Programming). We shall verify the correctness by computing and comparing optimal policies for a large number of unseen MDPs. If your code fails any test instances, you will be penalised based on the nature of the mistake made.

5 marks are allotted for the correctness of Task 2. Once again, we will run the encoder-planner-decoder sequence on a number of initial policies (with either player fixed) and verify if the policy you compute is indeed optimal.

Task 3 will be assessed for 5 marks. Your answer to the question on convergence, along with suitable proof, will carry 3 marks. We will also run task3.py to see your empirical demonstration of the claim, and reserve 2 marks for it.

The TAs and instructor may look at your source code to corroborate the results obtained by your program, and may also call you to a face-to-face session to explain your code.

Deadline and Rules

Your submission is due by 11.55 p.m., Monday, October 11. Finish working on your submission well in advance, keeping enough time to generate your data, compile the results, and upload to Moodle.

Your submission will not be evaluated (and will be given a score of zero) if it is not uploaded to Moodle by the deadline. Do not send your code to the instructor or TAs through any other channel. Requests to evaluate late submissions will not be entertained.

Your submission will receive a score of zero if your code does not execute on cs747 docker container. To make sure you have uploaded the right version, download it and check after submitting (but before the deadline, so you can handle any contingencies before the deadline lapses).

You are expected to comply with the rules laid out in the "Academic Honesty" section on the course web page, failing which you are liable to be reported for academic malpractice.

References for Linear Programming

For the Linear Programming part of the assignment, we recommend you to use the Python library PuLP. PuLP is convenient to use directly from Python code: here is a short tutorial and here is a reference. PuLP version 2.4 is installed in the CS 747 docker.