


Next: About this document ...
Up: $FILE
Previous: Unix Commands
Go to the CS101 home page.
- Download the fib and log programs (follow the lectures link to find these
files) and save as local files.
- Open the calculator applet (click on the resources link, to find
the calculator applet).
Run the applet (see handout given on day 1 for tips in case you have problems).
Open and run each of the above programs.
- Edit the programs to change the input values, and reload and rerun
the programs. Check that the correct value is produced for
for each input.
Testing the program with different input values
is an important part of programming. Make sure you test with
``special cases'', such as with input value 0, and in the case of
the log program, with powers of 10. Try fib with a large number
(say 40) and see what happens - use the execute up to line number option
to avoid stepping one line at a time.
Now write any one or more of the following programs; do as many
as time permits, but it is enough if you do one or two.
The programs will not count towards your grade, but you must submit
whatever you have done via moodle and you will get feedback.
Submit even if the program does not work (note that it doesn't work).
If you have more than one program to submit just put them all
in one file (one after the other) and submit the file.
You will not have time in the lab to finish all problems, but after the lab you can try writing programs for the other problems on paper. Note that  indicates easy,
indicates easy,  is medium and
is medium and  is hard, and it is enough for this
course if you are able to do the easy problems.
is hard, and it is enough for this
course if you are able to do the easy problems.
 Given a polynomial
Given a polynomial
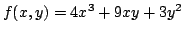 , and values for
, and values for
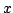 and
and 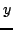 , compute
, compute 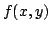 .
.
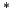 Given n, add up all powers of 2 from 1 to
Given n, add up all powers of 2 from 1 to 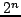 .
.
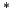 Given number
Given number 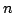 find value of
find value of 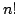
 Given numbers
Given numbers 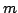 and
and 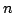 , compute
, compute 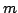 modulo
modulo 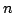 .
Note that CAL does not have a modulo (remainder) operator.
.
Note that CAL does not have a modulo (remainder) operator.
 Given a number
Given a number 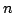 decide the number of bits required to represent this number in binary. For example, with input = 7, the
binary form (111) requires 3 bits.
decide the number of bits required to represent this number in binary. For example, with input = 7, the
binary form (111) requires 3 bits.
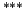 Given a decimal number between 0 and 63, print out its
(unsigned) binary representation. Since CAL does not support
binary really,
you will print out the corresponding decimal number made up of
1s and 0s, eg given 2, you will display 10, given 63 you will
display 11111.
Given a decimal number between 0 and 63, print out its
(unsigned) binary representation. Since CAL does not support
binary really,
you will print out the corresponding decimal number made up of
1s and 0s, eg given 2, you will display 10, given 63 you will
display 11111.
Make sure to add comments explaining how your program works.
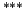 Given a decimal number of up to 5 digits consisting only
zeros and ones.
Then, assuming it as unsigned binary convert it to equivalent
decimal number.
For example, suppose the input is 1011 (decimal, as CAL accepts
only decimal numbers). Assuming it as binary equivalent, you would
have to output the decimal number 11.
Given a decimal number of up to 5 digits consisting only
zeros and ones.
Then, assuming it as unsigned binary convert it to equivalent
decimal number.
For example, suppose the input is 1011 (decimal, as CAL accepts
only decimal numbers). Assuming it as binary equivalent, you would
have to output the decimal number 11.
Make sure to add comments explaining how your program works.
 Easy
Easy  Medium
Medium  Hard
Hard



Next: About this document ...
Up: $FILE
Previous: Unix Commands
cs101 Lab
2007-08-06
![]() indicates easy,
indicates easy, ![]() is medium and
is medium and ![]() is hard, and it is enough for this
course if you are able to do the easy problems.
is hard, and it is enough for this
course if you are able to do the easy problems.
![]() Easy
Easy ![]() Medium
Medium ![]() Hard
Hard