← Home

Assignment Description

Due: Aug 1, 23:59:59 IST

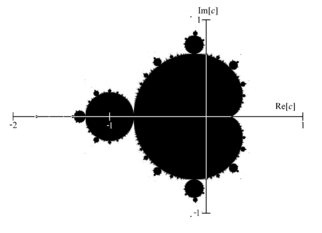
You will write a program that renders the Mandelbrot Set in a section of the complex plane.

Assignment Instructions

Your program has to compile to an executable named "mandelbrot" and take in four command line arguments, so that it can be used like this:

    ./mandelbrot lo.real lo.imag s output.png

    lo = (lo.real, lo.imag) is the lower-left corner of the output square in complex space
    s is the side length of the output square
    output.png is the filename of the resulting PNG image

This should produce a single square PNG image of 800px by 800px, a rendering of the section of the complex plane described by lo and s.

How to render the Mandelbrot Set

The Mandelbrot set is the set of complex points c such that iterating the function f(z) = z * z + c, starting from z = 0 does not cause it to diverge. In other words, the sequence f(0), f(f(0)), f(f(f(0)))... should not go to infinity.

Calculating the Mandelbrot set requires that you square a complex number. Remember that a complex number has a real and an imaginary part, so z = x + iy.

From this understanding of the Mandelbrot set (and a quick glance at Wikipedia) we can come up with an algorithm to draw the Mandelbrot set:

    For each pixel (row, col) in the image {

      Calculate the point c = x + iy on the complex plane that this pixel represents

      Let z = 0
      Repeat until an exit criterion has been met or we reached a maximum number of iterations {
        Update z to z * z + c
      }

      If the point has not escaped to infinity, color the pixel black
      If the point has escaped to infinity by our approximation, color it white

    }

Since we are calculating an infinite series, we need to approximate the result by cutting off the calculation at some point. If a point is inside the Mandelbrot set, we can keep iterating infinitely. To avoid this, we set a limit on the maximum number of iterations we will ever do. Choose this maximum value such that your picture looks like the example at the top of the page, but does not take excessively long to run (on my laptop it is generated in about one second). If a point is not in the Mandelbrot set, it will eventually move beyond the confines of the (-2, -2) to (2, 2) square within which the Mandelbrot set lies. This is the other exit criterion -- once the point we iterate on leaves this square, we know that it is not part of the Mandelbrot set and thus escapes to infinity.

Mapping pixels to points: Mapping the coordinates of a pixel in an image (specified by its row and column) to a point in the complex plane (specified by a real and an imaginary part) is slightly non-trivial.

They key thing to notice here is that each pixel is not a single point, but a little square region of the image. Let's look at a picture of what's going on:



Here, the entire image (a 5x3 grid of pixels) maps to the box (0, 0) to (1, 1) in the complex plane. Note that the corner points (0, 0), (0, 1), (1, 0) and (1, 1) lie on the boundary of the image. Each grid square (e.g. the colored ones) represents a single pixel. Its representative point is the red circle at its center, which is what we'll map to complex coordinates. A little math tells us that:

Row 0 maps to Y (imaginary) coordinate 1 - (0.5 / 3) (remember rows are top to bottom)
Row 2 maps to Y (imaginary) coordinate 0.5 / 3

... and similarly for the columns. A more general mapping is given in the source code. From this, you should work out a general formula for any pixel (row, col).

Extra Credit: At the minimum, we require that you render the Mandelbrot set in black and white, as in the example above (black for points inside the set, white for points outside). We will award extra credit for color renderings based on interesting color schemes. For example, coloring divergent points according to the speed of divergence or the number of iterations are known to give impressive colors.

Skeleton Code

Download the skeleton code here. (Jul 25, 2:00am)

The skeleton code consists of a file that you need to edit (mandelbrot.cpp), as well as a pair of files (stb_image_write.[ch]pp) for saving PNG images. In mandelbrot.cpp, please edit the following functions, exactly following the spec described in the function documentation:

    Complex pixelToPoint(int row, int col, Complex const & lo, double real_range, double imag_range);

    RGB8 getMandelbrotPointColor(Complex const & c);

Again, it is VERY IMPORTANT that you follow the spec, since we will independently test these functions using automatic scripts. It is ok to add additional functions, classes, constants etc, if needed, to the source file.

We provide a Makefile for Linux and macOS systems. You may need to explicitly install Clang/GCC on the former, and the Command Line Tools on the latter. For Windows, Visual Studio is a good buildsystem, though any other C++11-compliant compiler should work as well. We do not provide a VS project file, but just adding all three source files to a blank, new command-line project should do the trick. You do NOT need to submit this project file -- we should be able to build your program by just dropping your mandelbrot.cpp file into our buildsystem on Linux.

C++ Reference: I use the one at cplusplus.com. Note that the C++11 standard adds some features to the language -- it is ok to use them.

We also recommend looking at the Google C++ Style Guide. or other good coding standard. It will help you avoid the pitfalls of C++ and enable both you and others to read, understand and maintain your code later.

We do expect you to use the overloaded operators of the Complex class (a typedef for std::complex<double>) to do complex arithmetic. You WILL LOSE style points if you attempt to implement complex multiplication from scratch. Standard libraries exist so that we don't have to reinvent the wheel.

Submission Instructions

You need to submit both your results and source code. Your submission directory should be called a1, and it should contain:

Please do NOT include any other files!

You should zip this folder (do NOT use .tar, .tar.gz, .rar, .7z or any other format) and submit it on Moodle. If you log in to Moodle, you should find an assignment called "A1: Mandelbrot Set" set up. You can use "Add submission" to upload your zip file. You may upload multiple drafts, but remember to finalize your assignment with the "Submit Assignment" button before the deadline! After you finalize, you cannot make further changes without instructor permission.

Results: The text file results.txt should contain four lines. On each line, exactly write the command to reproduce one of your result images, in the order listed above. For instance, the whole.png image corresponds to the command:

./mandelbrot  -2  -2  4  whole.png

... This will be the first line of everyone's results.txt. The other three images are of your choosing, zoomed into interesting sections (for example, look at the Seahorse Valley of the set).

Note that if we execute the four commands in your results.txt one after the other, we should be able to exactly reproduce your result images.

Expected results

The basic functionality should not need more than 20 lines of C++ code. Getting a nice color scheme might require a few more lines. We expect the whole.png image to look like this (without the border):