Minimize sidelobe level of an array with arbitrary 2-D geometry

Jump to:     Source code     Text output      Plots     Library index

% "Convex optimization examples" lecture notes (EE364) by S. Boyd
% "Antenna array pattern synthesis via convex optimization"
% by H. Lebret and S. Boyd
% (figures are generated)
%
% Designs an antenna array such that:
% - it minimizes sidelobe level outside the beamwidth of the pattern
% - it has a unit sensitivity at some target direction
% - it has nulls (zero sensitivity) at specified direction(s) (optional)
%
% This is a convex problem (after sampling it can be formulated as an SOCP).
%
%   minimize   max |y(theta)|     for theta outside the beam
%       s.t.   y(theta_tar) = 1
%              y(theta_null) = 0  (optional)
%
% where y is the antenna array gain pattern (complex function) and
% variables are w (antenna array weights or shading coefficients).
% Gain pattern is a linear function of w: y(theta) = w'*a(theta)
% for some a(theta) describing antenna array configuration and specs.
%
% Written for CVX by Almir Mutapcic 02/02/06

% select array geometry
ARRAY_GEOMETRY = '2D_RANDOM';
% ARRAY_GEOMETRY = '1D_UNIFORM_LINE';
% ARRAY_GEOMETRY = '2D_UNIFORM_LATTICE';

% select if the optimal array pattern should enforce nulls or not
HAS_NULLS = 0; % HAS_NULLS = 1;

%********************************************************************
% problem specs
%********************************************************************
lambda = 1;           % wavelength
theta_tar = 60;       % target direction (should be an integer -- discretization)
half_beamwidth = 10;  % half beamwidth around the target direction

% angles where we want nulls (optional)
if HAS_NULLS
  theta_nulls = [95 110 120 140 225];
end

%********************************************************************
% random array of n antenna elements
%********************************************************************
if strcmp( ARRAY_GEOMETRY, '2D_RANDOM' )
  % set random seed to repeat experiments
  rand('state',0);

  % (uniformly distributed on [0,L]-by-[0,L] square)
  n = 40;
  L = 5;
  loc = L*rand(n,2);
  angleRange = 360;

%********************************************************************
% uniform 1D array with n elements with inter-element spacing d
%********************************************************************
elseif strcmp( ARRAY_GEOMETRY, '1D_UNIFORM_LINE' )
  % (unifrom array on a line)
  n = 30;
  d = 0.45*lambda;
  loc = [d*[0:n-1]' zeros(n,1)];
  angleRange = 180;

%********************************************************************
% uniform 2D array with m-by-m element with d spacing
%********************************************************************
elseif strcmp( ARRAY_GEOMETRY, '2D_UNIFORM_LATTICE' )
  m = 6; n = m^2;
  d = 0.45*lambda;

  loc = zeros(n,2);
  for x = 0:m-1
    for y = 0:m-1
      loc(m*y+x+1,:) = [x y];
    end
  end
  loc = loc*d;
  angleRange = 360;

else
  error('Undefined array geometry')
end

%********************************************************************
% construct optimization data
%********************************************************************
% build matrix A that relates w and y(theta), ie, y = A*w
theta = [1:angleRange]';
A = kron(cos(pi*theta/180), loc(:,1)') + kron(sin(pi*theta/180), loc(:,2)');
A = exp(2*pi*i/lambda*A);

% target constraint matrix
[diff_closest, ind_closest] = min( abs(theta - theta_tar) );
Atar = A(ind_closest,:);

% nulls constraint matrix
if HAS_NULLS
  Anull = []; ind_nulls = [];
  for k = 1:length(theta_nulls)
    [diff_closest, ind_closest] = min( abs(theta - theta_nulls(k)) );
    Anull = [Anull; A(ind_closest,:)];
    ind_nulls = [ind_nulls ind_closest];
  end
end

% stopband constraint matrix
ind = find(theta <= (theta_tar-half_beamwidth) | ...
           theta >= (theta_tar+half_beamwidth) );
if HAS_NULLS, ind = setdiff(ind,ind_nulls); end;
As = A(ind,:);

%********************************************************************
% optimization problem
%********************************************************************
cvx_begin
  variable w(n) complex
  minimize( max( abs(As*w) ) )
  subject to
    Atar*w == 1;   % target constraint
    if HAS_NULLS   % nulls constraints
      Anull*w == 0;
    end
cvx_end

% check if problem was successfully solved
disp(['Problem is ' cvx_status])
if ~strfind(cvx_status,'Solved')
  return
end

min_sidelobe_level = 20*log10( max(abs(As*w)) );
fprintf(1,'The minimum sidelobe level is %3.2f dB.\n\n',...
          min_sidelobe_level );

%********************************************************************
% plots
%********************************************************************
figure(1), clf
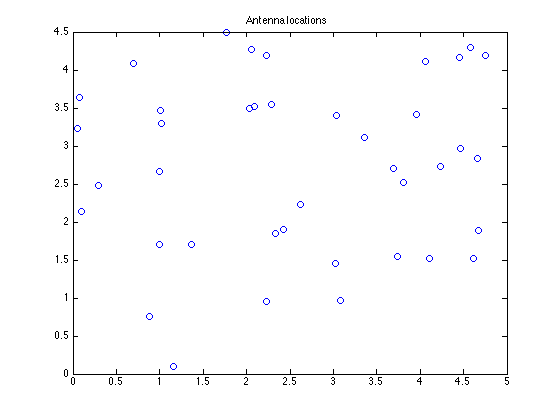
plot(loc(:,1),loc(:,2),'o')
title('Antenna locations')

% plot array pattern
if angleRange == 180,
    theta = [1:360]';
    A = [ A; -A ];
end
y = A*w;
figure(2), clf
ymin = floor(0.1*min_sidelobe_level)*10-10; ymax = 0;
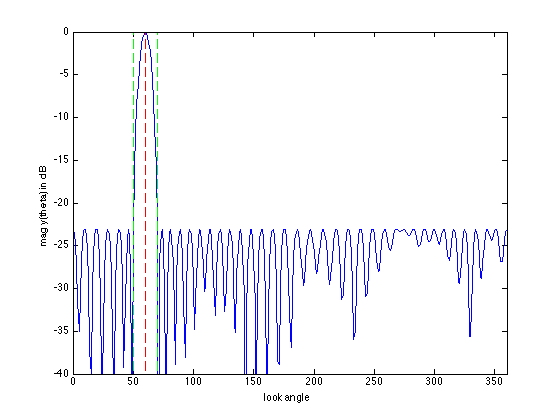
plot([1:360], 20*log10(abs(y)), ...
     [theta_tar theta_tar],[ymin ymax],'r--',...
     [theta_tar+half_beamwidth theta_tar+half_beamwidth],[ymin ymax],'g--',...
     [theta_tar-half_beamwidth theta_tar-half_beamwidth],[ymin ymax],'g--');
if HAS_NULLS % add lines that represent null positions
  hold on;
  for k = 1:length(theta_nulls)
    plot([theta_nulls(k) theta_nulls(k)],[ymin ymax],'m--');
  end
  hold off;
end
xlabel('look angle'), ylabel('mag y(theta) in dB');
axis([0 360 ymin ymax]);

% polar plot
figure(3), clf
zerodB = -ymin;
dBY = 20*log10(abs(y)) + zerodB;
ind = find( dBY <= 0 ); dBY(ind) = 0;
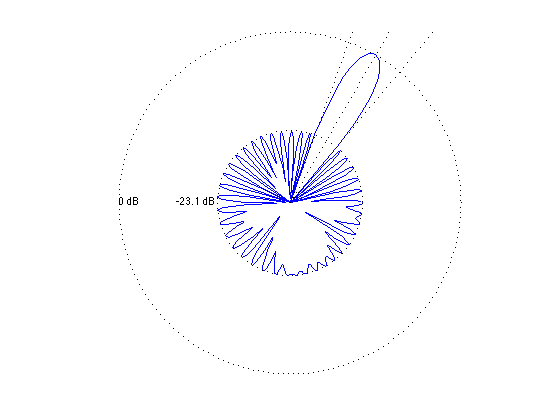
plot(dBY.*cos(pi*theta/180), dBY.*sin(pi*theta/180), '-');
axis([-zerodB zerodB -zerodB zerodB]), axis('off'), axis('square')
hold on
plot(zerodB*cos(pi*theta/180),zerodB*sin(pi*theta/180),'k:') % 0 dB
plot( (min_sidelobe_level + zerodB)*cos(pi*theta/180), ...
      (min_sidelobe_level + zerodB)*sin(pi*theta/180),'k:')  % min level
text(-zerodB,0,'0 dB')
tt = text(-(min_sidelobe_level + zerodB),0,sprintf('%0.1f dB',min_sidelobe_level));
set(tt,'HorizontalAlignment','right');
theta_1 = theta_tar+half_beamwidth;
theta_2 = theta_tar-half_beamwidth;
plot([0 55*cos(theta_tar*pi/180)], [0 55*sin(theta_tar*pi/180)], 'k:')
plot([0 55*cos(theta_1*pi/180)], [0 55*sin(theta_1*pi/180)], 'k:')
plot([0 55*cos(theta_2*pi/180)], [0 55*sin(theta_2*pi/180)], 'k:')
if HAS_NULLS % add lines that represent null positions
  for k = 1:length(theta_nulls)
    plot([0 55*cos(theta_nulls(k)*pi/180)], ...
         [0 55*sin(theta_nulls(k)*pi/180)], 'k:')
  end
end
hold off

 
Calling SDPT3: 1366 variables, 422 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 422
 dim. of socp   var  = 1023,   num. of socp blk  = 341
 dim. of linear var  = 341
 dim. of free   var  =  2 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|4.4e+02|2.1e+02|2.4e+05|-2.746283e-10  0.000000e+00| 0:0:00| chol  1  1 
 1|0.988|0.993|5.1e+00|1.7e+00|2.8e+03|-5.910542e-04 -3.754743e+01| 0:0:00| chol  1  1 
 2|0.996|1.000|1.8e-02|3.0e-02|4.3e+01|-1.073909e-04 -3.294803e+01| 0:0:00| chol  1  1 
 3|1.000|0.981|2.6e-06|7.1e-03|2.8e+00|-1.796667e-04 -2.767530e+00| 0:0:00| chol  1  1 
 4|1.000|0.889|6.0e-06|1.1e-03|6.9e-01|-3.329714e-03 -6.951011e-01| 0:0:00| chol  2  2 
 5|1.000|0.330|2.8e-06|7.2e-04|4.8e-01|-5.429149e-03 -4.885746e-01| 0:0:00| chol  2  2 
 6|1.000|0.198|3.0e-06|5.8e-04|4.0e-01|-9.246853e-03 -4.104552e-01| 0:0:00| chol  2  2 
 7|1.000|0.482|4.2e-07|3.0e-04|2.4e-01|-1.445314e-02 -2.511027e-01| 0:0:00| chol  2  2 
 8|0.886|0.301|2.3e-07|2.1e-04|1.7e-01|-2.381270e-02 -1.966532e-01| 0:0:00| chol  2  2 
 9|0.786|0.273|1.2e-07|1.5e-04|1.3e-01|-3.394599e-02 -1.629322e-01| 0:0:00| chol  2  3 
10|0.880|0.310|7.9e-08|1.1e-04|8.9e-02|-4.555408e-02 -1.348750e-01| 0:0:01| chol  2  2 
11|0.865|0.832|1.6e-08|3.2e-05|2.5e-02|-5.529792e-02 -8.055960e-02| 0:0:01| chol  2  2 
12|0.709|0.931|5.4e-09|7.8e-06|1.0e-02|-6.356599e-02 -7.375485e-02| 0:0:01| chol  2  2 
13|0.667|0.933|1.9e-09|3.1e-06|4.2e-03|-6.697687e-02 -7.115279e-02| 0:0:01| chol  2  2 
14|0.824|0.941|6.4e-10|1.3e-06|1.3e-03|-6.924836e-02 -7.050785e-02| 0:0:01| chol  3  2 
15|0.846|0.816|3.7e-10|3.8e-07|3.8e-04|-6.998889e-02 -7.036806e-02| 0:0:01| chol  3  3 
16|0.844|0.908|3.7e-10|1.1e-07|1.3e-04|-7.018825e-02 -7.032177e-02| 0:0:01| chol  3  3 
17|0.954|0.944|3.6e-10|4.0e-08|2.1e-05|-7.028439e-02 -7.030500e-02| 0:0:01| chol  3  4 
18|0.945|0.904|1.2e-09|6.3e-09|3.5e-06|-7.029929e-02 -7.030261e-02| 0:0:01| chol  5  5 
19|0.914|0.857|3.3e-09|1.1e-09|9.0e-07|-7.030163e-02 -7.030222e-02| 0:0:01| chol  6  5 
20|0.896|0.951|6.8e-09|3.3e-10|2.1e-07|-7.030246e-02 -7.030211e-02| 0:0:01| chol 10 12 
21|0.615|0.944|6.2e-09|2.6e-10|1.1e-07|-7.030271e-02 -7.030210e-02| 0:0:01| chol  9 10 
22|0.616|0.943|5.0e-09|3.8e-10|5.7e-08|-7.030275e-02 -7.030209e-02| 0:0:01| chol 11 10 
23|0.612|0.943|6.5e-09|5.6e-10|3.1e-08|-7.030268e-02 -7.030209e-02| 0:0:01| chol 
  linsysolve: Schur complement matrix not positive definite
  switch to LU factor. lu 12   3 
24|0.613|0.943|6.5e-09|8.4e-10|1.6e-08|-7.030281e-02 -7.030209e-02| 0:0:01|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 24
 primal objective value = -7.03028095e-02
 dual   objective value = -7.03020909e-02
 gap := trace(XZ)       = 1.63e-08
 relative gap           = 1.43e-08
 actual relative gap    = -6.30e-07
 rel. primal infeas     = 6.48e-09
 rel. dual   infeas     = 8.44e-10
 norm(X), norm(y), norm(Z) = 5.6e-01, 1.1e+02, 1.5e+00
 norm(A), norm(b), norm(C) = 1.7e+02, 2.0e+00, 2.4e+00
 Total CPU time (secs)  = 1.35  
 CPU time per iteration = 0.06  
 termination code       =  0
 DIMACS: 6.5e-09  0.0e+00  1.0e-09  0.0e+00  -6.3e-07  1.4e-08
-------------------------------------------------------------------
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.0703021
 
Problem is Solved
The minimum sidelobe level is -23.06 dB.