% Boyd & Vandenberghe "Convex Optimization"
% Joëlle Skaf - 04/24/08
% (a figure is generated)
%
% The investment strategy x that maximizes the long term growth rate
%           R = sum_{j=1}^m pi_j*log(p_j^Tx)
% is called the log-optimal investment strategy, and can be found by
% solving the optimization problem
%           maximize    sum_{j=1}^m pi_j log(p_j^Tx)
%           subject to  x >= 0, sum(x) = 1,
% where p_ij is the return of asset i over one period in scenario j and
% pi_j is the probability of scenario j. There are n assets and m scenarios.
% We consider the case of equiprobable scenarios.
%
% The log-optimal long term growth rate is found and compared to the one
% obtained with a uniform allocation strategy, i.e., x_i=(1/n).
% Sample trajectories ofthe accumulated wealth for the optimal strategy and
% the uniform one are plotted.


% Input data
P = [3.5000    1.1100    1.1100    1.0400    1.0100;
     0.5000    0.9700    0.9800    1.0500    1.0100;
     0.5000    0.9900    0.9900    0.9900    1.0100;
     0.5000    1.0500    1.0600    0.9900    1.0100;
     0.5000    1.1600    0.9900    1.0700    1.0100;
     0.5000    0.9900    0.9900    1.0600    1.0100;
     0.5000    0.9200    1.0800    0.9900    1.0100;
     0.5000    1.1300    1.1000    0.9900    1.0100;
     0.5000    0.9300    0.9500    1.0400    1.0100;
     3.5000    0.9900    0.9700    0.9800    1.0100];

[m,n] = size(P);
Pi = ones(m,1)/m;
x_unif = ones(n,1)/n; % uniform resource allocation

% Find the log-optimal investment policy
cvx_begin
    variable x_opt(n)
    maximize sum(Pi.*log(P*x_opt))
    sum(x_opt) == 1
    x_opt >= 0
cvx_end

% Long-term growth rates
R_opt = sum(Pi.*log(P*x_opt));
R_unif = sum(Pi.*log(P*x_unif));
display('The long term growth rate of the log-optimal strategy is: ');
disp(R_opt);
display('The long term growth rate of the uniform strategy is: ');
disp(R_unif);

% Generate random event sequences
rand('state',10);
N = 10;  % number of random trajectories
T = 200; % time horizon
w_opt = []; w_unif = [];
for i = 1:N
    events = ceil(rand(1,T)*m);
    P_event = P(events,:);
    w_opt = [w_opt [1; cumprod(P_event*x_opt)]];
    w_unif = [w_unif [1; cumprod(P_event*x_unif)]];
end

% Plot wealth versus time
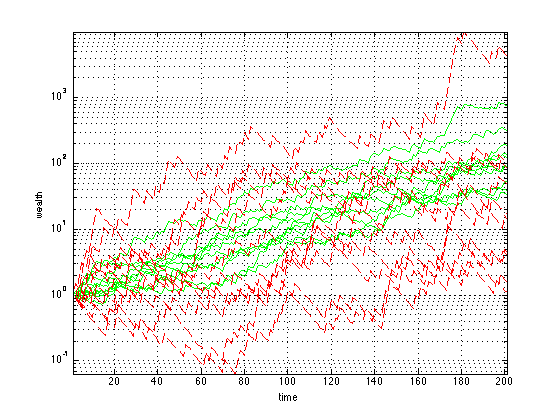
figure
semilogy(w_opt,'g')
hold on
semilogy(w_unif,'r--')
grid
axis tight
xlabel('time')
ylabel('wealth')

 
Successive approximation method to be employed.
   SDPT3 will be called several times to refine the solution.
   Original size: 35 variables, 21 equality constraints
   10 exponentials add 80 variables, 50 equality constraints
-----------------------------------------------------------------
 Cones  |             Errors              |
Mov/Act | Centering  Exp cone   Poly cone | Status
--------+---------------------------------+---------
 10/ 10 | 2.272e-01  3.277e-03  0.000e+00 | Solved
 10/ 10 | 2.176e-02  3.026e-05  0.000e+00 | Solved
  8/ 10 | 2.785e-03  4.952e-07  0.000e+00 | Solved
  0/  8 | 3.602e-04  8.044e-09  0.000e+00 | Solved
-----------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.0230783
 
The long term growth rate of the log-optimal strategy is: 
    0.0231

The long term growth rate of the uniform strategy is: 
    0.0114