% Figure 7.4
% Boyd & Vandenberghe "Convex Optimization"
% Original version by Lieven Vandenberghe
% Updated for CVX by Michael Grant, 2005-12-19

% Generate the data
P = [0.70  0.10
     0.20  0.10
     0.05  0.70
     0.05  0.10];
[n,m] = size(P);

% Construct the tradeoff curve by finding the
% the Pareto optimal deterministic detectors,
% which are the curve's vertices

nopts   = 1000;
weights = logspace(-5,5,nopts);
obj     = [0;1];
inds    = ones(n,1);

% minimize  -t1'*q1 - w*t2'*q2
% s.t.      t1+t2 = 1,  t1,t2 \geq 0

next = 2;
for i = 1 : nopts,
   PW = P * diag( [ 1 ; weights(i) ] );
   [ maxvals, maxinds ] = max( PW' );  % max elt in each row
   if (~isequal(maxinds', inds(:,next-1)))
       inds(:,next) = maxinds';
       T = zeros(m,n);
       for j=1:n
          T(maxinds(1,j),j) = 1;
       end;
       obj(:,next) = 1-diag(T*P);
       next = next+1;
   end;
end;
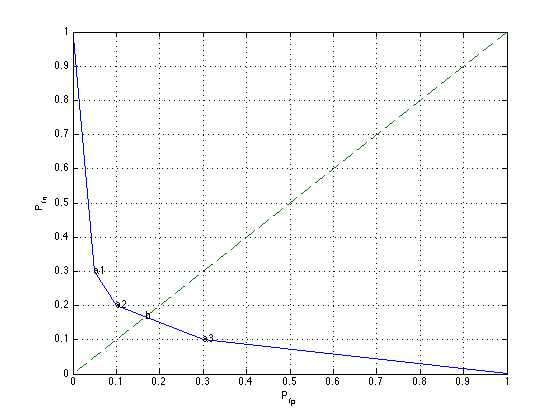
plot(obj(1,:), obj(2,:),[0 1], [0 1],'--');
grid on
for i=2:size(obj,2)-1
   text(obj(1,i),obj(2,i),['a', num2str(i-1)]);
end;

% Minimax detector: not deterministic

cvx_begin
    variables T( m, n ) D( m, m )
    minimize max( D(1,2), D(2,1) )
    subject to
        D == T * P;
        sum( T, 1 ) == 1;
        T >= 0;
cvx_end

objmp = 1 - diag( D );
text( objmp(1), objmp(2), 'b' );
xlabel('P_{fp}'); ylabel('P_{fn}');

%print -deps roc.eps

 
Calling SDPT3: 11 variables, 6 equality constraints
------------------------------------------------------------

 num. of constraints =  6
 dim. of linear var  = 10
 dim. of free   var  =  1 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|1.6e+01|1.3e+01|1.0e+03| 2.875957e-10  0.000000e+00| 0:0:00| chol  1  1 
 1|0.960|0.784|6.3e-01|2.9e+00|1.3e+02| 8.945382e+00 -3.154700e+01| 0:0:00| chol  1  1 
 2|1.000|0.972|1.2e-06|9.1e-02|1.6e+01| 6.618313e+00 -8.420478e+00| 0:0:00| chol  1  1 
 3|1.000|0.352|3.5e-07|6.0e-02|8.3e+00| 1.069569e+00 -6.764824e+00| 0:0:00| chol  1  1 
 4|1.000|0.911|1.8e-06|5.4e-03|7.6e-01| 4.837967e-01 -2.586458e-01| 0:0:00| chol  1  1 
 5|0.868|0.462|2.5e-07|2.9e-03|3.8e-01| 2.414092e-01 -1.231513e-01| 0:0:00| chol  1  1 
 6|1.000|0.693|8.5e-08|8.9e-04|1.1e-01| 1.874677e-01  8.179283e-02| 0:0:00| chol  1  1 
 7|1.000|0.591|6.2e-09|3.7e-04|3.9e-02| 1.691964e-01  1.312147e-01| 0:0:00| chol  1  1 
 8|0.989|0.952|1.9e-09|1.8e-05|1.8e-03| 1.667232e-01  1.649578e-01| 0:0:00| chol  1  1 
 9|0.989|0.989|1.1e-10|2.0e-07|2.1e-05| 1.666673e-01  1.666471e-01| 0:0:00| chol  1  1 
10|0.989|0.989|2.4e-12|5.1e-07|3.8e-07| 1.666667e-01  1.666664e-01| 0:0:00| chol  1  1 
11|1.000|0.989|6.8e-15|9.3e-09|8.6e-09| 1.666667e-01  1.666667e-01| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 11
 primal objective value =  1.66666668e-01
 dual   objective value =  1.66666663e-01
 gap := trace(XZ)       = 8.62e-09
 relative gap           = 6.46e-09
 actual relative gap    = 4.40e-09
 rel. primal infeas     = 6.79e-15
 rel. dual   infeas     = 9.32e-09
 norm(X), norm(y), norm(Z) = 1.9e+00, 7.5e-01, 8.9e-01
 norm(A), norm(b), norm(C) = 4.9e+00, 3.0e+00, 2.4e+00
 Total CPU time (secs)  = 0.12  
 CPU time per iteration = 0.01  
 termination code       =  0
 DIMACS: 1.0e-14  0.0e+00  1.1e-08  0.0e+00  4.4e-09  6.5e-09
-------------------------------------------------------------------
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.166667