% Section 8.4.1, Boyd & Vandenberghe "Convex Optimization"
% Almir Mutapcic - 10/05
% (a figure is generated)
%
% Given a finite set of points x_i in R^2, we find the minimum volume
% ellipsoid (described by matrix A and vector b) that covers all of
% the points by solving the optimization problem:
%
%           maximize     log det A
%           subject to   || A x_i + b || <= 1   for all i
%
% CVX cannot yet handle the logdet function, but this problem can be
% represented in an equivalent way as follows:
%
%           maximize     det(A)^(1/n)
%           subject to   || A x_i + b || <= 1   for all i
%
% The expression det(A)^(1/n) is SDP-representable, and is implemented
% by the MATLAB function det_rootn().

% Generate data
x = [ 0.55  0.0;
      0.25  0.35
     -0.2   0.2
     -0.25 -0.1
     -0.0  -0.3
      0.4  -0.2 ]';
[n,m] = size(x);

% Create and solve the model
cvx_begin
    variable A(n,n) symmetric
    variable b(n)
    maximize( det_rootn( A ) )
    subject to
        norms( A * x + b * ones( 1, m ), 2 ) <= 1;
cvx_end

% Plot the results
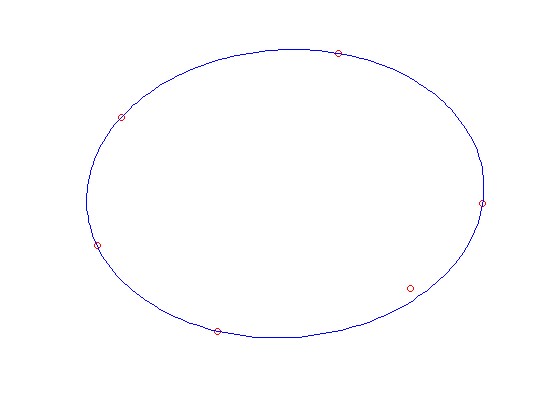
clf
noangles = 200;
angles   = linspace( 0, 2 * pi, noangles );
ellipse  = A \ [ cos(angles) - b(1) ; sin(angles) - b(2) ];
plot( x(1,:), x(2,:), 'ro', ellipse(1,:), ellipse(2,:), 'b-' );
axis off

 
Calling SDPT3: 38 variables, 16 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 16
 dim. of sdp    var  =  6,   num. of sdp  blk  =  2
 dim. of socp   var  = 18,   num. of socp blk  =  6
 dim. of linear var  =  7
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|1.8e+01|1.1e+01|1.4e+03| 2.078461e+01  0.000000e+00| 0:0:00| chol  1  1 
 1|1.000|0.738|8.9e-06|2.8e+00|4.2e+02| 7.162953e+01 -6.914125e+00| 0:0:00| chol  1  1 
 2|1.000|0.995|5.9e-06|2.3e-02|4.9e+01| 4.663101e+01  5.635756e-02| 0:0:00| chol  1  1 
 3|0.867|1.000|8.2e-07|1.0e-03|6.4e+00| 6.754724e+00  4.007027e-01| 0:0:00| chol  1  1 
 4|0.855|1.000|1.4e-07|1.0e-04|2.2e+00| 3.823699e+00  1.581767e+00| 0:0:00| chol  1  1 
 5|0.981|0.949|6.6e-09|1.5e-05|2.3e-01| 2.782621e+00  2.549170e+00| 0:0:00| chol  1  1 
 6|0.982|0.858|1.7e-09|2.9e-06|2.6e-02| 2.694716e+00  2.669164e+00| 0:0:00| chol  1  1 
 7|0.897|0.908|1.0e-09|3.6e-07|3.1e-03| 2.684875e+00  2.681819e+00| 0:0:00| chol  1  1 
 8|0.926|1.000|2.9e-09|1.0e-08|1.1e-03| 2.684388e+00  2.683302e+00| 0:0:00| chol  1  1 
 9|0.974|0.933|5.9e-10|1.9e-09|7.4e-05| 2.684001e+00  2.683927e+00| 0:0:00| chol  1  1 
10|0.991|0.975|5.0e-12|1.7e-10|2.4e-06| 2.683986e+00  2.683983e+00| 0:0:00| chol  1  1 
11|1.000|0.993|4.7e-14|2.1e-12|6.2e-08| 2.683985e+00  2.683985e+00| 0:0:00|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 11
 primal objective value =  2.68398542e+00
 dual   objective value =  2.68398536e+00
 gap := trace(XZ)       = 6.15e-08
 relative gap           = 9.67e-09
 actual relative gap    = 9.66e-09
 rel. primal infeas     = 4.70e-14
 rel. dual   infeas     = 2.11e-12
 norm(X), norm(y), norm(Z) = 3.1e+00, 6.1e+00, 1.0e+01
 norm(A), norm(b), norm(C) = 7.7e+00, 2.0e+00, 3.4e+00
 Total CPU time (secs)  = 0.26  
 CPU time per iteration = 0.02  
 termination code       =  0
 DIMACS: 4.7e-14  0.0e+00  3.6e-12  0.0e+00  9.7e-09  9.7e-09
-------------------------------------------------------------------
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +2.68399