% S. Boyd, et. al., "Convex Optimization of Graph Laplacian Eigenvalues"
% ICM'06 talk examples (www.stanford.edu/~boyd/cvx_opt_graph_lapl_eigs.html)
% Written for CVX by Almir Mutapcic 08/29/06
% (figures are generated)
%
% In this example we consider a graph described by the incidence matrix A.
% Each edge has a weight W_i, and we optimize various functions of the
% edge weights as described in the referenced paper; in particular,
%
% - the fastest distributed linear averaging (FDLA) problem (fdla.m)
% - the fastest mixing Markov chain (FMMC) problem (fmmc.m)
%
% Then we compare these solutions to the heuristics listed below:
%
% - maximum-degree heuristic (max_deg.m)
% - constant weights that yield fastest averaging (best_const.m)
% - Metropolis-Hastings heuristic (mh.m)

% generate a cut-grid graph example
[A,xy] = cut_grid_data;

% Compute edge weights: some optimal, some based on heuristics
[n,m] = size(A);

[ w_fdla, rho_fdla ] = fdla(A);
[ w_fmmc, rho_fmmc ] = fmmc(A);
[ w_md,   rho_md   ] = max_deg(A);
[ w_bc,   rho_bc   ] = best_const(A);
[ w_mh,   rho_mh   ] = mh(A);

tau_fdla = 1/log(1/rho_fdla);
tau_fmmc = 1/log(1/rho_fmmc);
tau_md   = 1/log(1/rho_md);
tau_bc   = 1/log(1/rho_bc);
tau_mh   = 1/log(1/rho_mh);

fprintf(1,'\nResults:\n');
fprintf(1,'FDLA weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fdla,tau_fdla);
fprintf(1,'FMMC weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fmmc,tau_fmmc);
fprintf(1,'M-H weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_mh,tau_mh);
fprintf(1,'MAX_DEG weights:\t rho = %5.4f \t tau = %5.4f\n',rho_md,tau_md);
fprintf(1,'BEST_CONST weights:\t rho = %5.4f \t tau = %5.4f\n',rho_bc,tau_bc);

% plot results
figure(1), clf
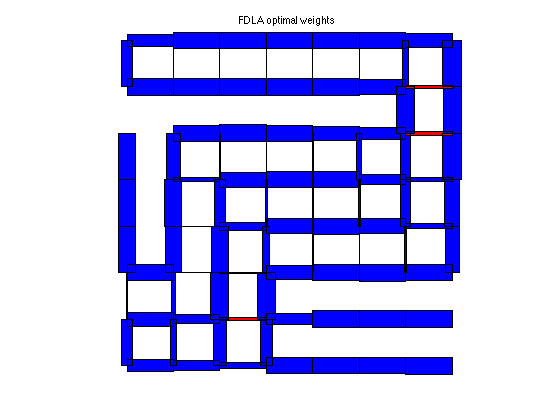
plotgraph(A,xy,w_fdla);
text(0.425,1.05,'FDLA optimal weights')

figure(2), clf
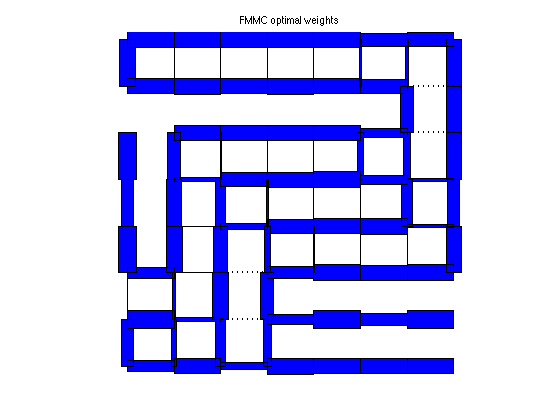
plotgraph(A,xy,w_fmmc);
text(0.425,1.05,'FMMC optimal weights')

figure(3), clf
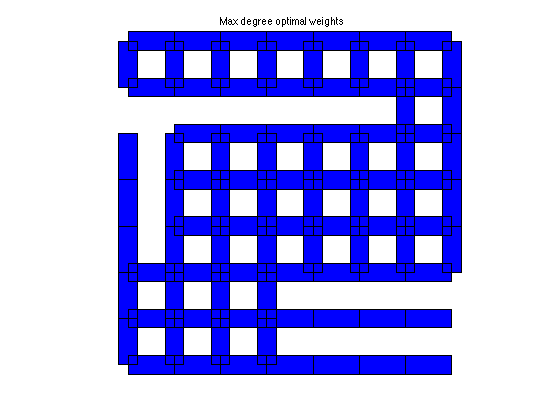
plotgraph(A,xy,w_md);
text(0.375,1.05,'Max degree optimal weights')

figure(4), clf
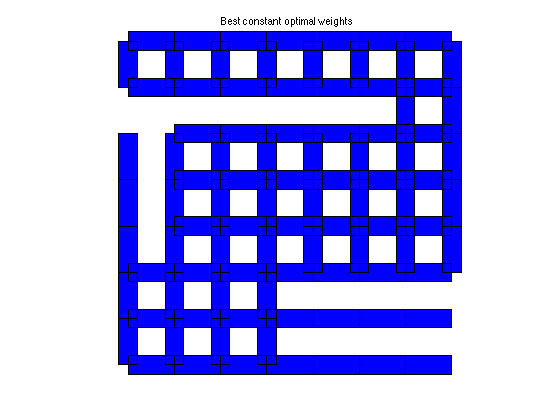
plotgraph(A,xy,w_bc);
text(0.375,1.05,'Best constant optimal weights')

figure(5), clf
plotgraph(A,xy,w_mh);
text(0.3,1.05,'Metropolis-Hastings optimal weights')

 
Calling SDPT3: 4184 variables, 120 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 120
 dim. of sdp    var  = 128,   num. of sdp  blk  =  2
 dim. of free   var  = 24 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|2.0e+03|3.4e+01|1.7e+05| 1.089043e-08  0.000000e+00| 0:0:00| chol  1  1 
 1|0.965|0.980|7.1e+01|7.5e-01|2.2e+03| 3.873783e+00 -1.102409e+01| 0:0:00| chol  1  1 
 2|0.994|0.995|4.4e-01|1.3e-02|2.2e+01| 1.728486e-02 -1.116953e+01| 0:0:00| chol  1  1 
 3|1.000|1.000|6.0e-04|1.0e-03|2.6e+00|-2.633304e-02 -2.603883e+00| 0:0:00| chol  1  1 
 4|1.000|0.826|4.7e-05|3.8e-04|8.4e-01|-2.380295e-01 -1.061296e+00| 0:0:00| chol  1  1 
 5|0.510|0.835|2.0e-05|8.0e-05|6.4e-01|-7.194634e-01 -1.357586e+00| 0:0:00| chol  2  1 
 6|0.950|0.372|1.9e-05|5.5e-05|2.9e-01|-9.186017e-01 -1.210926e+00| 0:0:00| chol  1  2 
 7|1.000|0.434|9.0e-06|3.5e-05|1.5e-01|-9.545688e-01 -1.105679e+00| 0:0:00| chol  1  1 
 8|1.000|0.494|1.7e-06|1.9e-05|7.2e-02|-9.697835e-01 -1.041325e+00| 0:0:00| chol  1  1 
 9|1.000|0.290|3.6e-07|1.4e-05|4.7e-02|-9.779319e-01 -1.024303e+00| 0:0:00| chol  2  1 
10|1.000|0.184|2.0e-07|1.2e-05|3.8e-02|-9.796448e-01 -1.017426e+00| 0:0:00| chol  2  2 
11|0.979|0.656|1.2e-07|4.0e-06|1.2e-02|-9.862540e-01 -9.979613e-01| 0:0:01| chol  2  2 
12|1.000|0.148|2.4e-07|1.9e-05|1.2e-02|-9.861327e-01 -9.965449e-01| 0:0:01| chol  1  2 
13|1.000|0.967|1.7e-08|2.0e-05|1.2e-03|-9.877992e-01 -9.885658e-01| 0:0:01| chol  1  2 
14|0.944|0.966|9.9e-10|1.9e-06|1.3e-04|-9.881871e-01 -9.883052e-01| 0:0:01| chol  2  2 
15|1.000|0.975|5.2e-12|2.1e-07|1.2e-05|-9.882813e-01 -9.882926e-01| 0:0:01| chol  1  2 
16|1.000|0.984|8.0e-12|1.9e-08|4.5e-07|-9.882915e-01 -9.882919e-01| 0:0:01| chol  2  2 
17|1.000|0.984|1.3e-12|7.5e-10|2.1e-08|-9.882919e-01 -9.882919e-01| 0:0:01|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 17
 primal objective value = -9.88291864e-01
 dual   objective value = -9.88291884e-01
 gap := trace(XZ)       = 2.07e-08
 relative gap           = 6.96e-09
 actual relative gap    = 6.82e-09
 rel. primal infeas     = 1.27e-12
 rel. dual   infeas     = 7.54e-10
 norm(X), norm(y), norm(Z) = 9.9e-01, 6.8e+00, 1.3e+01
 norm(A), norm(b), norm(C) = 3.5e+01, 2.0e+00, 1.2e+01
 Total CPU time (secs)  = 0.76  
 CPU time per iteration = 0.04  
 termination code       =  0
 DIMACS: 1.3e-12  0.0e+00  4.5e-09  0.0e+00  6.8e-09  7.0e-09
-------------------------------------------------------------------
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.988292
 
 
Calling SDPT3: 4366 variables, 143 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 143
 dim. of sdp    var  = 128,   num. of sdp  blk  =  2
 dim. of linear var  = 159
 dim. of free   var  = 47 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|2.1e+03|7.8e+01|1.8e+06| 4.543368e+02  0.000000e+00| 0:0:00| chol  1  1 
 1|0.792|0.933|4.3e+02|5.4e+00|4.2e+04| 8.746282e+02 -1.017808e+01| 0:0:00| chol  1  1 
 2|0.894|0.971|4.5e+01|2.2e-01|2.3e+03| 7.232508e+02 -1.051730e+01| 0:0:00| chol  1  1 
 3|0.943|0.889|2.6e+00|3.2e-02|2.0e+02| 1.138259e+02 -1.091174e+01| 0:0:00| chol  1  1 
 4|0.996|0.762|9.9e-03|8.3e-03|1.7e+01| 6.171212e+00 -9.192580e+00| 0:0:00| chol  1  1 
 5|0.958|0.889|4.1e-04|2.9e-03|1.4e+00| 1.601739e-01 -1.159879e+00| 0:0:00| chol  1  1 
 6|0.532|0.514|1.9e-04|1.5e-03|9.9e-01|-2.051399e-01 -1.170931e+00| 0:0:00| chol  1  1 
 7|1.000|0.329|3.6e-08|1.1e-03|3.5e-01|-7.741526e-01 -1.114688e+00| 0:0:00| chol  1  1 
 8|1.000|0.544|2.3e-08|4.8e-04|1.3e-01|-9.079428e-01 -1.037563e+00| 0:0:00| chol  1  1 
 9|0.937|0.465|7.6e-09|2.6e-04|5.8e-02|-9.549597e-01 -1.011399e+00| 0:0:00| chol  1  1 
10|0.839|0.405|2.8e-09|1.5e-04|2.8e-02|-9.745665e-01 -1.001890e+00| 0:0:01| chol  1  1 
11|0.897|0.342|1.0e-09|9.4e-05|1.5e-02|-9.826287e-01 -9.976445e-01| 0:0:01| chol  1  1 
12|0.946|0.945|3.7e-10|1.6e-05|3.6e-03|-9.861534e-01 -9.896008e-01| 0:0:01| chol  2  2 
13|0.937|0.935|6.4e-11|3.6e-06|1.5e-03|-9.876189e-01 -9.891192e-01| 0:0:01| chol  1  2 
14|0.907|0.888|8.9e-11|1.5e-06|3.7e-04|-9.885403e-01 -9.888995e-01| 0:0:01| chol  2  2 
15|0.938|0.933|5.5e-11|3.7e-07|1.8e-04|-9.886851e-01 -9.888664e-01| 0:0:01| chol  2  2 
16|1.000|0.949|7.5e-10|1.9e-07|6.2e-05|-9.887810e-01 -9.888403e-01| 0:0:01| chol  2  2 
17|1.000|0.958|3.8e-10|6.2e-08|1.7e-05|-9.888136e-01 -9.888302e-01| 0:0:01| chol  2  2 
18|1.000|0.959|1.1e-10|1.7e-08|4.5e-06|-9.888228e-01 -9.888272e-01| 0:0:01| chol  2  3 
19|1.000|0.959|1.1e-10|4.6e-09|1.2e-06|-9.888253e-01 -9.888264e-01| 0:0:01| chol  3  4 
20|1.000|0.956|5.7e-10|1.3e-09|3.7e-07|-9.888259e-01 -9.888262e-01| 0:0:01| chol  5  4 
21|1.000|0.958|8.7e-10|3.9e-10|1.0e-07|-9.888261e-01 -9.888262e-01| 0:0:01| chol  5  7 
22|1.000|0.955|4.0e-10|1.4e-10|3.1e-08|-9.888261e-01 -9.888262e-01| 0:0:01|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 22
 primal objective value = -9.88826133e-01
 dual   objective value = -9.88826162e-01
 gap := trace(XZ)       = 3.08e-08
 relative gap           = 1.03e-08
 actual relative gap    = 9.75e-09
 rel. primal infeas     = 3.99e-10
 rel. dual   infeas     = 1.36e-10
 norm(X), norm(y), norm(Z) = 1.0e+00, 3.8e+00, 1.4e+01
 norm(A), norm(b), norm(C) = 3.6e+01, 2.0e+00, 1.3e+01
 Total CPU time (secs)  = 1.10  
 CPU time per iteration = 0.05  
 termination code       =  0
 DIMACS: 4.0e-10  0.0e+00  8.6e-10  0.0e+00  9.8e-09  1.0e-08
-------------------------------------------------------------------
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.988826
 

Results:
FDLA weights:		 rho = 0.9883 	 tau = 84.9099
FMMC weights:		 rho = 0.9888 	 tau = 88.9938
M-H weights:		 rho = 0.9917 	 tau = 120.2442
MAX_DEG weights:	 rho = 0.9927 	 tau = 136.7523
BEST_CONST weights:	 rho = 0.9921 	 tau = 126.3450