% S. Boyd, et. al., "Convex Optimization of Graph Laplacian Eigenvalues"
% ICM'06 talk examples (www.stanford.edu/~boyd/cvx_opt_graph_lapl_eigs.html)
% Written for CVX by Almir Mutapcic 08/29/06
% (figures are generated)
%
% In this example we consider a graph described by the incidence matrix A.
% Each edge has a weight W_i, and we optimize various functions of the
% edge weights as described in the referenced paper; in particular,
%
% - the fastest distributed linear averaging (FDLA) problem (fdla.m)
% - the fastest mixing Markov chain (FMMC) problem (fmmc.m)
%
% Then we compare these solutions to the heuristics listed below:
%
% - maximum-degree heuristic (max_deg.m)
% - constant weights that yield fastest averaging (best_const.m)
% - Metropolis-Hastings heuristic (mh.m)

% randomly generate a graph with 50 nodes and 200 edges
% and make it pretty for plotting
n = 50; threshold = 0.2529;
rand('state',209);
xy = rand(n,2);

angle = 10*pi/180;
Rotate = [ cos(angle) sin(angle); -sin(angle) cos(angle) ];
xy = (Rotate*xy')';

Dist = zeros(n,n);
for i=1:(n-1);
  for j=i+1:n;
    Dist(i,j) = norm( xy(i,:) - xy(j,:) );
  end;
end;
Dist = Dist + Dist';
Ad = Dist < threshold;
Ad = Ad - eye(n);
m = sum(sum(Ad))/2;

% find the incidence matrix
A = zeros(n,m);
l = 0;
for i=1:(n-1);
  for j=i+1:n;
    if Ad(i,j)>0.5
      l = l + 1;
      A(i,l) =  1;
      A(j,l) = -1;
    end;
  end;
end;
A = sparse(A);

% Compute edge weights: some optimal, some based on heuristics
[n,m] = size(A);

[ w_fdla, rho_fdla ] = fdla(A);
[ w_fmmc, rho_fmmc ] = fmmc(A);
[ w_md,   rho_md   ] = max_deg(A);
[ w_bc,   rho_bc   ] = best_const(A);
[ w_mh,   rho_mh   ] = mh(A);

tau_fdla = 1/log(1/rho_fdla);
tau_fmmc = 1/log(1/rho_fmmc);
tau_md   = 1/log(1/rho_md);
tau_bc   = 1/log(1/rho_bc);
tau_mh   = 1/log(1/rho_mh);

eig_opt  = sort(eig(eye(n) - A * diag(w_fdla) * A'));
eig_fmmc = sort(eig(eye(n) - A * diag(w_fmmc) * A'));
eig_mh   = sort(eig(eye(n) - A * diag(w_mh)   * A'));
eig_md   = sort(eig(eye(n) - A * diag(w_md)   * A'));
eig_bc   = sort(eig(eye(n) - A * diag(w_bc)   * A'));

fprintf(1,'\nResults:\n');
fprintf(1,'FDLA weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fdla,tau_fdla);
fprintf(1,'FMMC weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fmmc,tau_fmmc);
fprintf(1,'M-H weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_mh,tau_mh);
fprintf(1,'MAX_DEG weights:\t rho = %5.4f \t tau = %5.4f\n',rho_md,tau_md);
fprintf(1,'BEST_CONST weights:\t rho = %5.4f \t tau = %5.4f\n',rho_bc,tau_bc);

% plot results
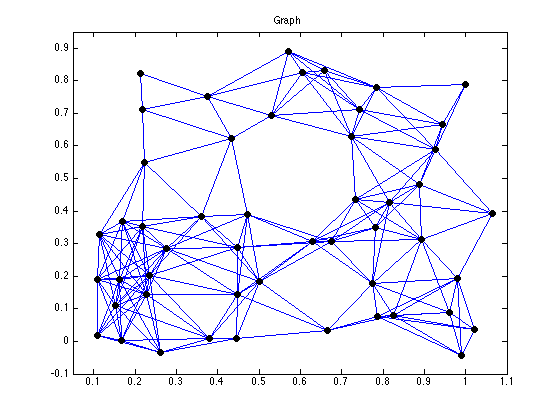
figure(1), clf
gplot(Ad,xy);
hold on;
plot(xy(:,1), xy(:,2), 'ko','LineWidth',4, 'MarkerSize',4);
axis([0.05 1.1 -0.1 0.95]);
title('Graph')
hold off;

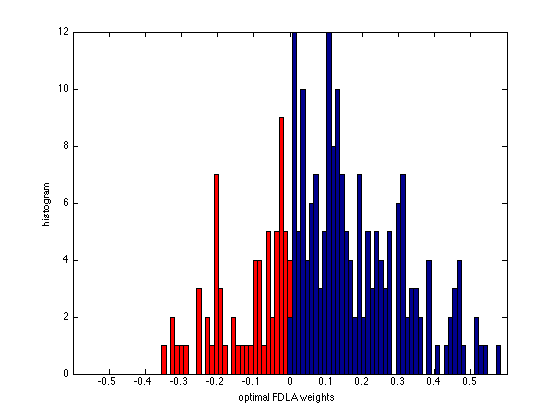
figure(2), clf
v_fdla = [w_fdla; diag(eye(n) - A*diag(w_fdla)*A')];
[ifdla, jfdla, neg_fdla] = find( v_fdla.*(v_fdla < -0.001 ) );
v_fdla(ifdla) = [];
wbins = [-0.6:0.012:0.6];
hist(neg_fdla,wbins); hold on,
h = findobj(gca,'Type','patch');
set(h,'FaceColor','r')
hist(v_fdla,wbins); hold off,
axis([-0.6 0.6 0 12]);
xlabel('optimal FDLA weights');
ylabel('histogram');

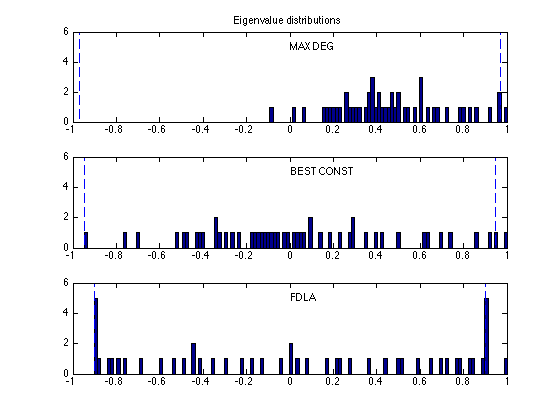
figure(3), clf
xbins = (-1:0.015:1)';
ymax  = 6;
subplot(3,1,1)
hist(eig_md, xbins); hold on;
max_md = max(abs(eig_md(1:n-1)));
plot([-max_md -max_md],[0 ymax], 'b--');
plot([ max_md  max_md],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'MAX DEG');
title('Eigenvalue distributions')
subplot(3,1,2)
hist(eig_bc, xbins); hold on;
max_opt = max(abs(eig_bc(1:n-1)));
plot([-max_opt -max_opt],[0 ymax], 'b--');
plot([ max_opt  max_opt],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'BEST CONST');
subplot(3,1,3)
hist(eig_opt, xbins); hold on;
max_opt = max(abs(eig_opt(1:n-1)));
plot([-max_opt -max_opt],[0 ymax], 'b--');
plot([ max_opt  max_opt],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'FDLA');

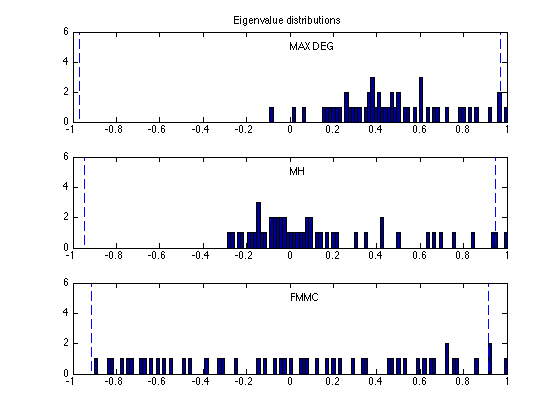
figure(4), clf
xbins = (-1:0.015:1)';
ymax  = 6;
subplot(3,1,1)
hist(eig_md, xbins); hold on;
max_md = max(abs(eig_md(1:n-1)));
plot([-max_md -max_md],[0 ymax], 'b--');
plot([ max_md  max_md],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'MAX DEG');
title('Eigenvalue distributions')
subplot(3,1,2)
hist(eig_mh, xbins); hold on;
max_opt = max(abs(eig_mh(1:n-1)));
plot([-max_opt -max_opt],[0 ymax], 'b--');
plot([ max_opt  max_opt],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'MH');
subplot(3,1,3)
hist(eig_fmmc, xbins); hold on;
max_opt = max(abs(eig_fmmc(1:n-1)));
plot([-max_opt -max_opt],[0 ymax], 'b--');
plot([ max_opt  max_opt],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'FMMC');

figure(5), clf
v_fmmc = [w_fmmc; diag(eye(n) - A*diag(w_fmmc)*A')];
[ifmmc, jfmmc, nonzero_fmmc] = find( v_fmmc.*(v_fmmc > 0.001 ) );
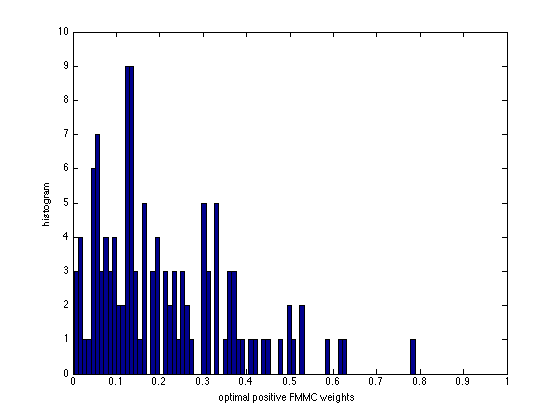
hist(nonzero_fmmc,80);
axis([0 1 0 10]);
xlabel('optimal positive FMMC weights');
ylabel('histogram');

figure(6), clf
An = abs(A*diag(w_fmmc)*A');
An = (An - diag(diag(An))) > 0.0001;
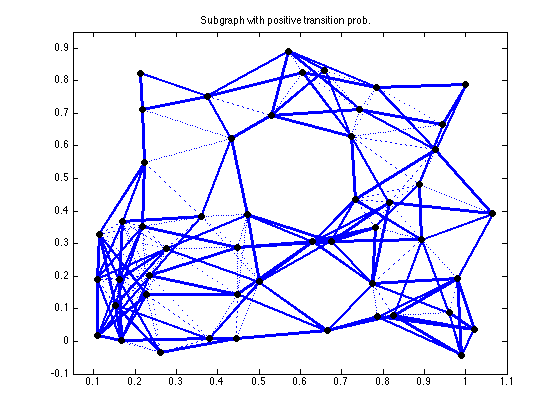
gplot(An,xy,'b-'); hold on;
h = findobj(gca,'Type','line');
set(h,'LineWidth',2.5)
gplot(Ad,xy,'b:');
plot(xy(:,1), xy(:,2), 'ko','LineWidth',4, 'MarkerSize',4);
axis([0.05 1.1 -0.1 0.95]);
title('Subgraph with positive transition prob.')
hold off;

 
Calling SDPT3: 2598 variables, 249 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 249
 dim. of sdp    var  = 100,   num. of sdp  blk  =  2
 dim. of free   var  = 48 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|1.3e+03|1.1e+02|1.0e+06|-3.054372e+01  0.000000e+00| 0:0:00| chol  1  1 
 1|0.925|0.974|9.6e+01|3.2e+00|8.5e+03| 1.302102e+01 -1.190896e+01| 0:0:00| chol  1  1 
 2|0.989|0.993|1.1e+00|4.9e-02|6.1e+01| 1.181474e-01 -1.229355e+01| 0:0:00| chol  1  1 
 3|1.000|1.000|4.3e-04|3.0e-03|6.7e+00| 6.215167e-03 -6.559567e+00| 0:0:00| chol  2  1 
 4|1.000|0.845|2.2e-04|8.0e-04|1.1e+00|-2.516558e-02 -1.084935e+00| 0:0:01| chol  1  1 
 5|0.635|0.437|8.1e-05|5.1e-04|6.3e-01|-5.388222e-01 -1.140827e+00| 0:0:01| chol  1  1 
 6|0.847|0.366|1.7e-05|3.4e-04|3.1e-01|-7.743386e-01 -1.064714e+00| 0:0:01| chol  1  1 
 7|0.915|0.609|3.6e-06|1.4e-04|1.0e-01|-8.637981e-01 -9.610145e-01| 0:0:01| chol  1  1 
 8|1.000|0.284|4.5e-07|9.9e-05|6.3e-02|-8.838014e-01 -9.438500e-01| 0:0:01| chol  1  1 
 9|1.000|0.430|2.8e-07|5.6e-05|3.3e-02|-8.939475e-01 -9.254959e-01| 0:0:01| chol  1  1 
10|1.000|0.414|8.1e-08|3.3e-05|1.8e-02|-8.984543e-01 -9.157209e-01| 0:0:01| chol  2  2 
11|1.000|0.379|2.2e-08|5.1e-05|1.1e-02|-9.003200e-01 -9.105304e-01| 0:0:01| chol  1  1 
12|1.000|0.915|1.2e-09|3.0e-05|1.7e-03|-9.013297e-01 -9.028095e-01| 0:0:02| chol  2  1 
13|1.000|0.898|9.3e-11|4.6e-06|3.5e-04|-9.018416e-01 -9.021701e-01| 0:0:02| chol  2  2 
14|0.988|0.933|1.1e-10|9.3e-07|5.7e-05|-9.020349e-01 -9.020887e-01| 0:0:02| chol  2  2 
15|1.000|0.961|1.4e-09|1.5e-07|8.8e-06|-9.020714e-01 -9.020798e-01| 0:0:02| chol  3  3 
16|1.000|0.962|3.0e-09|2.4e-08|1.5e-06|-9.020774e-01 -9.020788e-01| 0:0:02| chol  5  5 
17|1.000|0.963|5.3e-09|4.0e-09|2.4e-07|-9.020785e-01 -9.020787e-01| 0:0:02| chol  9 10 
18|1.000|0.969|5.7e-09|7.0e-10|3.1e-08|-9.020786e-01 -9.020787e-01| 0:0:02|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 18
 primal objective value = -9.02078640e-01
 dual   objective value = -9.02078663e-01
 gap := trace(XZ)       = 3.08e-08
 relative gap           = 1.10e-08
 actual relative gap    = 8.16e-09
 rel. primal infeas     = 5.72e-09
 rel. dual   infeas     = 6.96e-10
 norm(X), norm(y), norm(Z) = 9.6e-01, 7.0e+00, 1.1e+01
 norm(A), norm(b), norm(C) = 4.7e+01, 2.0e+00, 9.3e+00
 Total CPU time (secs)  = 2.46  
 CPU time per iteration = 0.14  
 termination code       =  0
 DIMACS: 5.7e-09  0.0e+00  3.3e-09  0.0e+00  8.2e-09  1.1e-08
-------------------------------------------------------------------
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.902079
 
 
Calling SDPT3: 2849 variables, 250 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 250
 dim. of sdp    var  = 100,   num. of sdp  blk  =  2
 dim. of linear var  = 250
 dim. of free   var  = 49 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|1.3e+03|1.1e+02|2.0e+06| 1.568490e+02  0.000000e+00| 0:0:00| chol  1  1 
 1|0.764|0.926|3.0e+02|8.0e+00|5.3e+04| 7.806708e+02 -1.228578e+01| 0:0:00| chol  1  1 
 2|0.901|0.968|3.0e+01|3.2e-01|2.6e+03| 8.418946e+02 -1.205433e+01| 0:0:00| chol  1  1 
 3|0.909|0.868|2.7e+00|6.3e-02|4.4e+02| 2.796621e+02 -1.295101e+01| 0:0:00| chol  1  1 
 4|0.995|0.607|1.3e-02|2.6e-02|5.1e+01| 3.057448e+01 -1.225165e+01| 0:0:01| chol  1  1 
 5|1.000|0.914|1.5e-05|5.0e-03|3.6e+00| 1.699810e+00 -1.702361e+00| 0:0:01| chol  1  1 
 6|1.000|0.632|5.0e-07|1.9e-03|1.5e+00| 4.796350e-01 -1.001701e+00| 0:0:01| chol  1  1 
 7|0.297|0.324|3.2e-07|1.3e-03|1.2e+00| 4.287331e-02 -1.160830e+00| 0:0:01| chol  1  1 
 8|0.925|0.231|3.6e-08|9.6e-04|5.0e-01|-6.307222e-01 -1.117206e+00| 0:0:01| chol  1  1 
 9|0.988|0.371|1.2e-08|6.1e-04|2.7e-01|-7.857468e-01 -1.048841e+00| 0:0:01| chol  1  1 
10|0.691|0.436|6.7e-09|3.4e-04|1.7e-01|-8.292146e-01 -9.936525e-01| 0:0:01| chol  1  1 
11|0.842|0.267|1.9e-09|2.5e-04|1.1e-01|-8.664913e-01 -9.741859e-01| 0:0:02| chol  1  1 
12|0.770|0.330|8.4e-10|1.7e-04|7.4e-02|-8.836940e-01 -9.561709e-01| 0:0:02| chol  1  1 
13|0.865|0.284|2.4e-10|1.2e-04|5.0e-02|-8.960108e-01 -9.454383e-01| 0:0:02| chol  1  1 
14|0.922|0.347|8.0e-11|7.8e-05|3.2e-02|-9.043659e-01 -9.357673e-01| 0:0:02| chol  1  1 
15|1.000|0.345|2.8e-11|5.6e-05|2.0e-02|-9.095103e-01 -9.291849e-01| 0:0:02| chol  1  1 
16|1.000|0.940|2.5e-11|2.3e-05|4.4e-03|-9.126087e-01 -9.167670e-01| 0:0:02| chol  1  1 
17|1.000|0.940|2.0e-11|5.0e-06|1.3e-03|-9.142866e-01 -9.156062e-01| 0:0:02| chol  2  2 
18|1.000|0.941|3.9e-12|1.6e-06|3.8e-04|-9.149180e-01 -9.152851e-01| 0:0:02| chol  2  2 
19|1.000|0.942|5.6e-12|4.3e-07|1.5e-04|-9.150589e-01 -9.152072e-01| 0:0:03| chol  2  2 
20|1.000|0.959|2.0e-11|1.7e-07|3.7e-05|-9.151297e-01 -9.151653e-01| 0:0:03| chol  2  2 
21|1.000|0.972|3.5e-11|4.2e-08|6.3e-06|-9.151478e-01 -9.151540e-01| 0:0:03| chol  2  2 
22|1.000|0.976|3.9e-11|7.3e-09|8.1e-07|-9.151511e-01 -9.151519e-01| 0:0:03| chol  4  3 
23|1.000|0.986|4.3e-11|9.4e-10|3.1e-08|-9.151515e-01 -9.151515e-01| 0:0:03|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 23
 primal objective value = -9.15151520e-01
 dual   objective value = -9.15151550e-01
 gap := trace(XZ)       = 3.10e-08
 relative gap           = 1.09e-08
 actual relative gap    = 1.05e-08
 rel. primal infeas     = 4.31e-11
 rel. dual   infeas     = 9.37e-10
 norm(X), norm(y), norm(Z) = 9.4e-01, 2.8e+00, 1.1e+01
 norm(A), norm(b), norm(C) = 4.7e+01, 2.0e+00, 9.6e+00
 Total CPU time (secs)  = 3.20  
 CPU time per iteration = 0.14  
 termination code       =  0
 DIMACS: 4.3e-11  0.0e+00  4.6e-09  0.0e+00  1.0e-08  1.1e-08
-------------------------------------------------------------------
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.915152
 

Results:
FDLA weights:		 rho = 0.9021 	 tau = 9.7037
FMMC weights:		 rho = 0.9152 	 tau = 11.2783
M-H weights:		 rho = 0.9489 	 tau = 19.0839
MAX_DEG weights:	 rho = 0.9706 	 tau = 33.5236
BEST_CONST weights:	 rho = 0.9470 	 tau = 18.3549