% Written for CVX by Kwangmoo Koh - 12/10/07
%
% The problem of estimating underlying trends in time series data arises in
% a variety of disciplines. The l1 trend filtering method produces trend
% estimates x that are piecewise linear from the time series y.
%
% The l1 trend estimation problem can be formulated as
%
%    minimize    (1/2)*||y-x||^2+lambda*||Dx||_1,
%
% with variable x , and problem data y and lambda, with lambda >0.
% D is the second difference matrix, with rows [0... -1 2 -1 ...0]
%
% CVX is not optimized for the l1 trend filtering problem.
% For large problems, use l1_tf (www.stanford.edu/~boyd/l1_tf/).

% load time series data
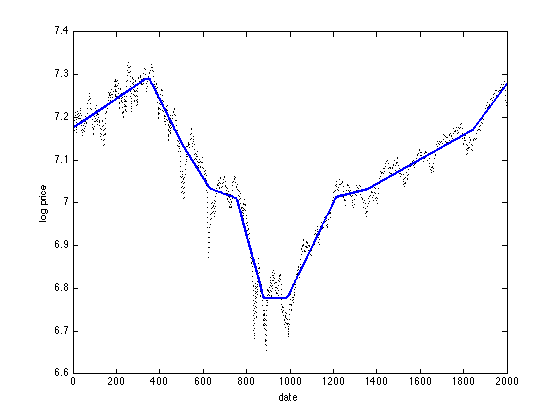
y = csvread('snp500.txt'); % log price of snp500
n = length(y);

% form second difference matrix
e = ones(n,1);
D = spdiags([e -2*e e], 0:2, n-2, n);

% set regularization parameter
lambda = 50;

% solve l1 trend filtering problem
cvx_begin
    variable x(n)
    minimize( 0.5*sum_square(y-x)+lambda*norm(D*x,1) )
cvx_end

% plot estimated trend with original signal
figure(1);
plot(1:n,y,'k:','LineWidth',1.0); hold on;
plot(1:n,x,'b-','LineWidth',2.0); hold off;
xlabel('date'); ylabel('log price');

 
Calling SDPT3: 5998 variables, 1999 equality constraints
------------------------------------------------------------

 num. of constraints = 1999
 dim. of socp   var  = 5998,   num. of socp blk  = 1999
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
    NT      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|2.0e+01|4.4e+01|6.4e+06| 1.413023e+05  0.000000e+00| 0:0:00| spchol  1  1 
 1|1.000|0.990|6.9e-06|4.6e-01|2.0e+05| 1.350438e+05 -1.049768e+03| 0:0:00| spchol  1  1 
 2|1.000|0.981|3.3e-06|9.1e-03|1.4e+04| 1.391107e+04 -2.044949e+01| 0:0:00| spchol  1  1 
 3|0.976|1.000|1.8e-06|2.1e-05|3.3e+02| 3.308001e+02 -7.132347e-01| 0:0:00| spchol  1  1 
 4|0.791|1.000|4.7e-06|2.4e-06|7.9e+01| 7.921631e+01  3.597732e-01| 0:0:00| spchol  1  1 
 5|0.879|0.776|7.8e-07|1.2e-06|2.1e+01| 2.193851e+01  7.904977e-01| 0:0:00| spchol  1  1 
 6|0.686|0.454|3.1e-07|8.3e-07|9.6e+00| 1.059057e+01  9.496103e-01| 0:0:00| spchol  1  1 
 7|0.634|0.493|1.5e-07|4.8e-07|5.1e+00| 6.224659e+00  1.075590e+00| 0:0:00| spchol  1  1 
 8|1.000|0.467|3.6e-08|2.9e-07|1.5e+00| 2.660531e+00  1.177521e+00| 0:0:00| spchol  1  1 
 9|0.597|0.769|4.0e-08|7.4e-08|7.6e-01| 2.088589e+00  1.326237e+00| 0:0:00| spchol  1  1 
10|0.958|0.676|1.7e-09|3.2e-08|1.9e-01| 1.569314e+00  1.378039e+00| 0:0:00| spchol  1  1 
11|0.745|0.795|4.3e-10|6.9e-09|7.1e-02| 1.468227e+00  1.396971e+00| 0:0:00| spchol  1  2 
12|0.645|0.713|1.5e-10|2.1e-09|3.4e-02| 1.433864e+00  1.400142e+00| 0:0:00| spchol  1  2 
13|0.772|0.854|3.5e-11|3.3e-10|1.1e-02| 1.412357e+00  1.401233e+00| 0:0:00| spchol  2  2 
14|0.702|0.779|1.0e-11|8.0e-11|4.7e-03| 1.406181e+00  1.401526e+00| 0:0:00| spchol  2  1 
15|0.876|0.877|5.5e-12|1.2e-11|9.4e-04| 1.402540e+00  1.401600e+00| 0:0:00| spchol  2  2 
16|0.559|0.946|9.4e-13|1.7e-12|5.0e-04| 1.402114e+00  1.401616e+00| 0:0:00| spchol  2  2 
17|0.565|0.994|1.6e-12|1.0e-12|2.6e-04| 1.401883e+00  1.401618e+00| 0:0:00| spchol  2  2 
18|0.564|1.000|3.2e-12|1.0e-12|1.4e-04| 1.401759e+00  1.401618e+00| 0:0:00| spchol  2  2 
19|0.565|1.000|9.2e-12|1.0e-12|7.5e-05| 1.401694e+00  1.401618e+00| 0:0:00| spchol  2  2 
20|0.558|1.000|1.8e-11|1.5e-12|4.1e-05| 1.401659e+00  1.401618e+00| 0:0:00| spchol  2  2 
21|0.560|1.000|1.5e-13|2.2e-12|2.2e-05| 1.401640e+00  1.401618e+00| 0:0:00| spchol  2  2 
22|0.553|1.000|4.7e-11|1.0e-12|1.2e-05| 1.401630e+00  1.401618e+00| 0:0:00| spchol  2  2 
23|0.555|1.000|3.8e-11|1.5e-12|6.4e-06| 1.401625e+00  1.401618e+00| 0:0:00| spchol  2  2 
24|0.557|1.000|2.8e-11|2.2e-12|3.5e-06| 1.401622e+00  1.401618e+00| 0:0:00| spchol  2  2 
25|0.559|1.000|2.2e-11|3.4e-12|1.9e-06| 1.401620e+00  1.401618e+00| 0:0:01| spchol  2  2 
26|0.561|1.000|6.5e-12|4.4e-12|1.0e-06| 1.401619e+00  1.401618e+00| 0:0:01| spchol  2  2 
27|0.562|1.000|8.5e-12|1.3e-12|5.4e-07| 1.401619e+00  1.401618e+00| 0:0:01| spchol  2  2 
28|0.564|1.000|3.9e-11|1.7e-12|2.9e-07| 1.401618e+00  1.401618e+00| 0:0:01| spchol  2  2 
29|0.565|1.000|8.8e-12|2.5e-12|1.5e-07| 1.401618e+00  1.401618e+00| 0:0:01| spchol  2  2 
30|0.566|0.975|1.0e-12|1.8e-12|8.2e-08| 1.401618e+00  1.401618e+00| 0:0:01| spchol  2  2 
31|0.567|0.967|6.5e-13|1.1e-12|4.4e-08| 1.401618e+00  1.401618e+00| 0:0:01|
  stop: max(relative gap, infeasibilities) < 1.49e-08
-------------------------------------------------------------------
 number of iterations   = 31
 primal objective value =  1.40161820e+00
 dual   objective value =  1.40161815e+00
 gap := trace(XZ)       = 4.36e-08
 relative gap           = 1.15e-08
 actual relative gap    = 1.15e-08
 rel. primal infeas     = 6.45e-13
 rel. dual   infeas     = 1.06e-12
 norm(X), norm(y), norm(Z) = 2.1e+00, 1.5e+03, 2.7e+03
 norm(A), norm(b), norm(C) = 1.2e+02, 2.2e+00, 2.2e+03
 Total CPU time (secs)  = 0.65  
 CPU time per iteration = 0.02  
 termination code       =  0
 DIMACS: 7.2e-13  0.0e+00  4.6e-11  0.0e+00  1.1e-08  1.1e-08
-------------------------------------------------------------------
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +1.40162