
(a) Original Cornell room.
|

(b) Rendering using AR.
|
Figure 1: The Cornell room, assumed to have a window. The figure on the left shows the standard room lit by an interior light source. At a different point of day, the room is lit by an unexpected light source with arbitrary shape through the window. We would like to bind a solution based on the first one, instead of starting a new solution based on a new patch.
|

(a) An office with two flat screen monitors, presumably with screen savers on.
|

(b) The appearance changes because mouse motion causes the windows to break out the screen saver mode. Note that the positions of these new "light sources" is not known apriori.
|
Figure 2: Two different states of an office. The solution on the right is incrementally computed based on the illumination in the first by Algorithm AR.
| |

(a) Original Cornell room.
|

(b) Rendering using AR.
|
Figure 3: Light filters through the southern wall onto the blue wall. The resulting scene is rendered incrementally in the first method on the right.
|

(a) Original Cornell room.
|

(b) Rendering using AR.
|
Figure 4: A second light appears on the eastern wall.
|

(a) Original Cornell room.
|

(b) Rendering using AR.
|
Figure 5: The light on the blue wall disappears to reflect the passage of time.
|

(a) Original Cornell room.
|
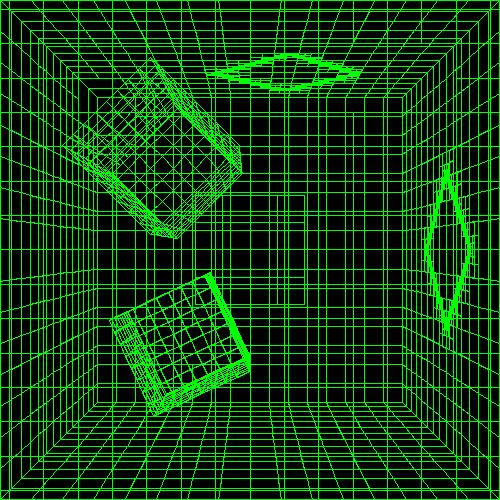
(b) Rendering using AR.
|
Figure 6: A wireframe is shown to visualize how adaptive refine(appearing on the right) further refines Previous Approach.
|