 |
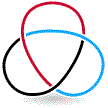
This is another method used to distinguish one knot from the other. To understand the concept of tricolorability we have to define a strand. A strand is a piece of string in a knot that goes from one under crossing to the next over crossing. Tricolorability uses this fact, i.e. if each strands in the projection of the knot can be colored in one of the three different colors. The thing to note is that each crossing should have either three different colors coming together or the same color. Also the other limitation when using this rule is that atleast two out of the three colors should be used in the knot. This helps us distinguish and safely conclude that the unknot is not a knot but just a knotted loop in a circle as it fails the tricolorability test. The next example shows that the trefoil knot is tricolorable by showing that two different projections of the trefoil are tricolorable. So the trefoil knot is not the unknot as it is tricolorable, using this test we have proved that the trefoil is different from the unknot.
It should also be noted that the Reidemeister moves also preserve the tricolorability test.