CS628 Projects
- Given a process algebra description (text string) , the aim is to
write a program that can decompose this process into elementary
components like merge, arbiter, etc. Then, the original process and
decomposed process should be checked for trace equivalence by using
CWB.
- Given a process algebra P, and a library L of process algebra, we
intend to decompose the process P into the processes from the library
L and elementary components like merge, arbiter, etc. Write a program
to do this decomposition.
- Given a proces algebra P and a set of production rules PRs,
verify the correctness of PRs by feeding both PRs and the process
algebra to CWB and check their trace equivalence. Represent the
process P using PRs in verificationtool SPIN. Verify properties (which
are evident from the process algebra) of the process using SPIN.
- Given a proces algebra P and a set of production rules PRs,
verify the correctness of PRs by feeding both PRs and the process
algebra to CWB and check their trace equivalence. Represent the
process P using PRs in verificationtool NuSMV. Verify properties
(which are evident from the process algebra) of the process using
NuSMV.
- Given a process algebra, set of production rules PRs and some
timing information about occurence of events in the process, obtain a
simplified set ofproduction rules.
Example : Consider a process algebraic description P = (a? [] b? ) ->
c? -> d! Suppose the timing information provided is a event b occurs
between any two events on a. Then this information can be exploited to
obtain a simpler set of production rules for process P.
- Given an STG without choice (but with concurrency), the aim is to
partition it structurally into approximately equal parts. You have to
then verify their trace equivalence. Structural partitioning involves
looking at the STG only (and not the corresponding STD) and break it
up into smaller STGs. Thus, the input to your program will be an STG,
and the output will be two or more STGs. Tool to be used in
Petrify. Petrify allows you to represent STGs easily.
- Given an STG without choice (but with concurrency), the aim is to
partition it into two or more STGs based on the state-space traversal
of the original STG. You have to then verify their trace
equivalence. State-space based partitioning of an STG involves looking
at the corresponding STD and then partitioning that STD into
approximately equal smaller STDs. Thus, the input to your program
will be an STG, and the output will be two or more STGs(not STDs).
Tool to be used in Petrify.
- Given an STG (with both choice and concurrency), you have to
model it using the tool NuSMV. NuSMV is a Symbolic model
checker. NuSMV allows to check finite state systems against
specifications in the temporal logic CTL. You have to then verify
interesting properties on the STG. Thus, the input to your program
will be an STG, and output will be the modelling of that STG in the
NuSMV input-language.
- Given an STG, and some additional timing information, you have to
simplify the given STG to another STG. The timing information will
give the relative ordering between certain events. The simplification
will be based on the state-space traversal of the original
STG(i.e. based on the corresponding STD). You have to then use the
tool CWB to verify whether all the traces of the simplified STG are
contained in the set of traces of the original STG. Thus, the input to
your program will be an STG, and the output will be a simplified
STG.
- Given an STG, and some additional timing information, you have to
simplify the given STG to another STG. The timing information will
give the relative ordering between certain events. The simplification
will be based on the structure of the given STG (and not its
state-space). You have to then use the tool Petrify to verify whether
all the traces of the simplified STG are contained in the set of
traces of the original STG. Thus, the input to your program will be
an STG, and the output will be a simplified STG.
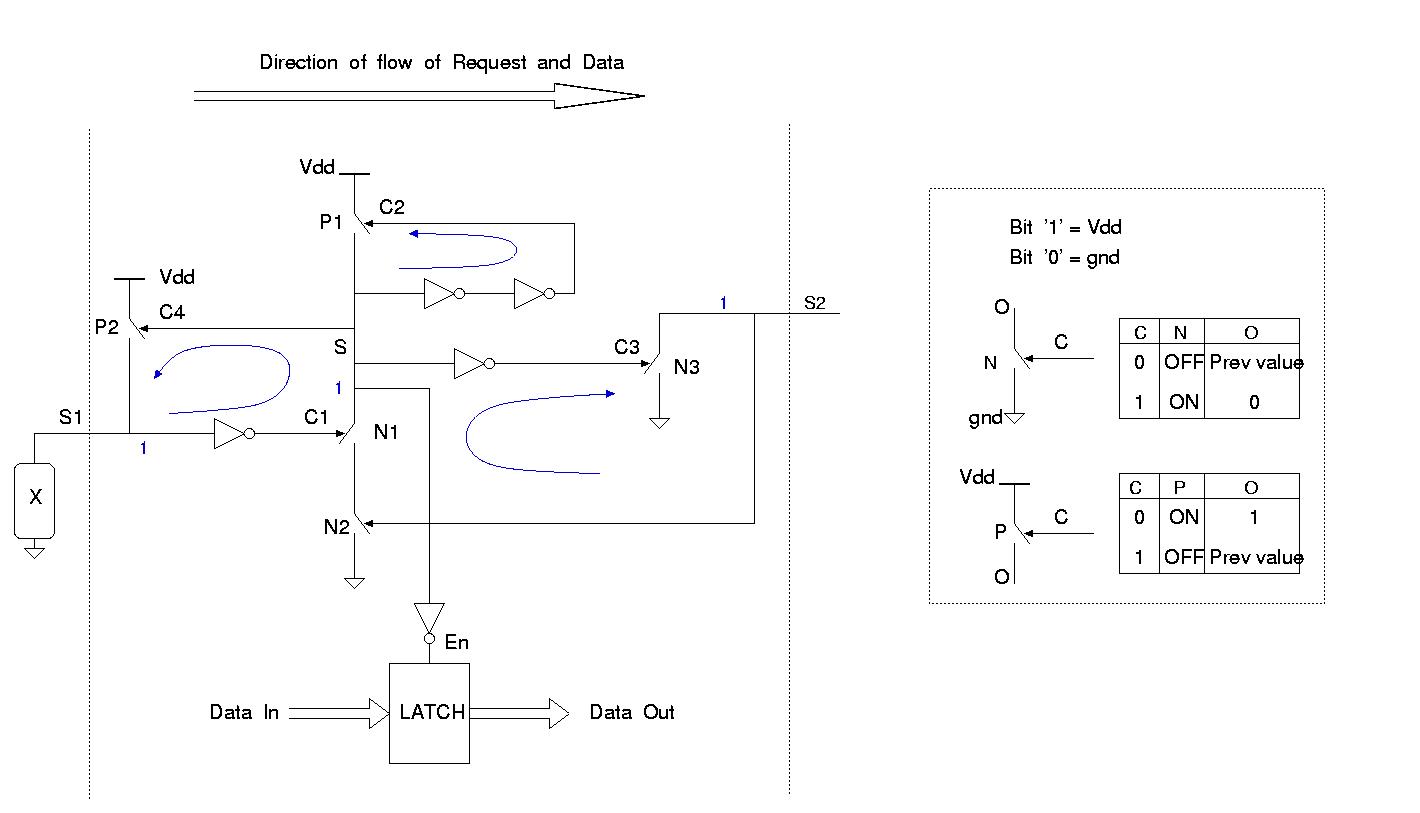
- GasP, shown in Fig. 1, is a fast asynchronous FIFO cell.
Each cell is composed of the control circuit and data latching
circuit. Several such cells can be cascaded to build linear and
non-linear pipelines. If every switch (P/N) and the inverter shown in
Fig. 1 has a time of operation as 1 time unit, then it takes 6 time
units for transfering a request from S1 to S2, i.e. 6 gate delays for
a GasP cell operation.
The working of the GasP is as follows. Let, S1, S and S2 be referred
to as conductors and C1, C2 and C3 the control signals for different
switches. The operation of switch P and N is shown in the
figure. When C is 1(0), N(P) is ON and O becomes 0(1). When C is 0(1),
N(P) is OFF and O remains in its previous state. The initial values of
the conductors S1, S and S2 are all 1 (shown in blue).
Thus, P1, P2, N1 and N3 are OFF while N2 is ON. To begin data/request
transfer, X(some circuit) pulls S1 low in the first stage of the
FIFO. Following sequence of events happen after S1 is pulled
low:
S1=0 -> N1 is turned ON -> N1 and N2 pull S low -> S=0.
After S becomes 0 following 4 things happen :
- S=0 -> C4=0 -> P2 is turned ON -> S1 is reset to 1. This turns
off N1.
- S=0 -> C2=0 -> P1 is turned ON -> S is reset to 1.
- S=0 -> C3=1 -> N3 is turned ON -> is pulled to 0 which turns off
N2.
- A pulse is generated on En due to 1 -> 0 -> 1 transition on
S. This pulse enables a latch to latch the input data. The data is
transferred from first stage to the next and the first stage is reset
(as it becomes empty). It can now take on the next request. In a
similar fashion request/data propogates through the entire pipeline
when several GasP stages are connected.
Modeling GasP using NuSMV : Use NuSMV to model a GasP
cell. The model should be such that it should allow you to build FIFOs
by simply interconnecting several such cells. Finally, you should be
able to verify certain interesting properties of GasP circuits in
NuSMV. You may assume each gate delay to be of 1 time unit.
- Modeling GasP using Kronos/Uppal : Use Kronos or Uppal to
model a GasP cell. Kronos/Uppal allows you to verify real-time
systems. Thus, your GasP cell model should take actual gate (switches
and inverters) delays. The model should be such that it should allow
you to build FIFOs by simply interconnecting several such
cells. Finally, you should be able to verify interesting properties of
GasP circuits.
- Performance analysis of linear and non-linear GasP pipelines
using NuSMV : Use NuSMV to model each GasP cell. You can model the
GasP cell at a coarser level if required, i.e., you may not model each
switch/inverter separately but can combine several gates/funtion as
one element with appropriate delay. The GasP model should be such that
it allows you to cascade several GasP cells to form different
configurations such as simple linear pipelines, branch-and-join
pipelines, circular (round robin) pipelines etc. For such
configurations we would like to verify interesting properties for the
pipelines. We would also like to do timing analysis of these
configurations using NuSMV.
- Timing analysis of XBM Machines :Write a program that
takes as input XBM state transition diagram and generates as output,
set of input vectors that can be used to perform timing analysis of
the XBMs. A 0,1,X-simulator can be assumed to be available.
- Automatic Decomposition of XBMs into communicating XBMs :
Write a progam that takes as input XBM and decomposes it into
two or more communicating XBMs.
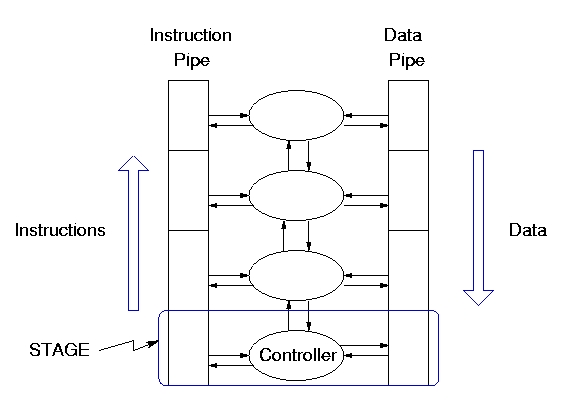
- Modeling and Analysis of Counterflow pipeline processor (CFPP)
architecture : Fig. 2 shows the basic CFPP architecture. Model
one complete stage of CFPP using NuSMV or SPIN. The model should be
such that it allows you to build a pipeline by interconnecting several
such stages. You should be able to verify interesting properties of
CFPP.
- Optimization and Analysis of CFPP : There are conditions
when CFPP can get blocked. We would like to alter the original CFPP
and develop a new CFPP called as opti-CFPP which contains an extra
data pipe(scratch pipe). The scratch pipe has a nice property that
data is never stalled in this pipe and it continously keeps moving
down. You need to develop the opti-CFPP architecture containing a
scratch pipe and a new controller and argue about its performance
versus performance of the original CFPP.
- Modeling Timed XBMs : Use Kronos to model timed XBMs
and verify interesting properties on it.
- You have to implement the Grid communication
protocol in a 3-D network using network sockets. You are well aware of
this problem from your first homework, only that you have to extend it
to 3-D and actually implement it using network sockets. You should
then be able to actually do the timing analysis on the grid.

