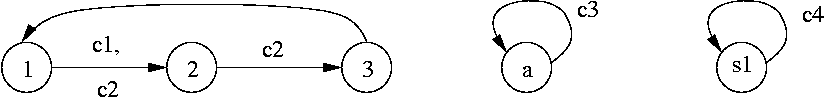Brief on Automata Composition
There are three kinds of signals associated with every module: inputs,
outputs and clocks. The behavior of every module is described by the
sequence of events that take place on these signals and can be most
easily represented by an automaton. Thus, given a GALS system, we use
automata to describe each of the communicating modules. Apart from
this, there are one or more automata that describe the relations
between the clocks. If the clocks are unrelated then they could be
represented by a set of independent automata. Some of these clock
automata are shown in the figure below:
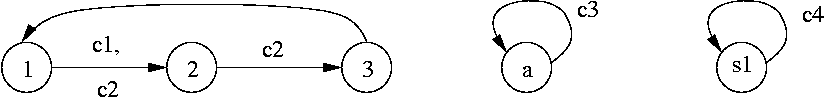
The composition of asynchronous automata A and B is their product A x
B. An asynchronous signal is defined as one which has no
relation with any of the clocks. However, in most communicating
modules, the output signals of the module are generated synchronously
by the corresponding module clock. We refer to such signals as
synchronous signals. A synchronous signal is generated
synchronously by exactly one clock. Special care needs to be
taken when composing automata with a mix of synchronous and asynchronous
events.
The composition algorithm works as follows:
- The initial state is the product of the initial states of all
the automata.
- From every composed state Si = (a1,a2,...,ak),
the next transition labeled by event, say e1, takes us to
Si+1 = (b1, a2, ... , bk). In the states corresponding
to Si, e1 may be enabled in some automata and not in other
automata. The states where e1 was enabled move on to the next state,
whereas in those automata where e1 is not enabled the state does not
change. For example, state a2 of a certain automaton remains as it is,
whereas a1 of some other automaton goes to b1, and ak goes to bk, on
e1. This step is recursively repeated till all the states are
exhausted to get the composed automaton. This procedure gives an
asynchronous composition of 2 or more
automata.
(c) As we
mentioned above, in our automata there are synchronous signals apart
from the asynchronous ones. These need to be specially handled. We'll
take an example to explain why synchronous signals need to be handled
separately by our algorithm.
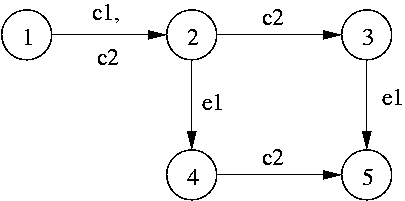
Let e1 be
an output event of some module M1 and let us assume that it is
synchronous to clock c1 of the same module M1. Let c2 be some other
clock in the system. As shown in the automaton we go from state
1 to state 2 on c1 and c2. From state 2 there are two transition that
are enabled, e1 and c2. If e1 is taken we go to state 4. However, if
c2 is taken then we go from state 3 to state 4. From here e1
should not be allowed. This is because when c2 is taken it means that
one clock period of c2 (T of c2) has elapsed after c1 took place. If
e1 is synchronous with c1 then it has to be generated after small time
after the clock c1. (This small time is negligible as compared to a
clock period). If e1 happens after state 3, then e1 can no longer be
considered synchronous to c1. This will violate the protocol of module
M1. Hence, e1 from state 3 has to be disabled. For taking care
of such cases we define a field called synchronous_proximity at every composite state. This
field stores all the clocks
that have just transitioned. A synchronous event can take
place from a composite state only if its corresponding clock is found
in the synchronous_proximity
list.
- The
synchronous_proximity for the
starting state is null, as no
clocks have transitioned yet.
- The synchronous_proximity for the composite
state Si
= (a1,a2,...,ak) is the union of all clocks that have transitioned
from the starting state of each automaton to reach this
state.
- The
synchronous_proximity for the next
composite
state Si+1
= (b1, a2, ... , bk)
from Si
= (a1,a2,...,ak) is calculated as follows. If
the synchronous_proximity for
Si is
{c1, c2} then
the synchronous_proximity for
Si+1
is
- {c1, c2}, if some
asynchronous event, say e2, takes place
from
Si
,
- {c1, c2, c3}, if clock c3 event
takes place
from Si.
c3 can be
considered like an asynchronous signal
here.
- {c1, c2}, if e1 event which is
synchronous to c1 takes place
from Si
. The synchronous_proximity is preserved
when a synchronous event takes
place. Also, e1
event can take place only if c1 is present in
the
synchronous_proximity
list of
Si.
- {c2}, if c2 event takes place from
Si.
Since a clock event c2 has taken place one clock period has elapsed
since Si
and hence all the events synchronous to the clocks in the
synchronous_proximity of
Si can
no longer take place. Only those events synchronous to c2 can take
place. Hence
the synchronous_proximity for
Si
is just {c2}.
The other important thing that needs to
be noted is that whenever a state is reached from two different paths
then the synchronous_proximities
obtained from the different paths
should be the same. If not, the state is treated as inconsistent and
is discarded by our current tool. Since the states as well as
the number of clocks are finite in most practical implementations, we
would like to extend our tool so that the state information includes
synchronous_proximity also
to avoid inconsistent states.
For every automaton it is important that there is a separate
starting state which is never reached again when the automaton is
traversed. This is important as we have considered its
synchronous_proximity to
be null i.e. {}. So, if this state is reached by any other path it
will be marked inconsistent as described above.
The
example
shown on the website can provides important guidelines to the users of
our
automata composition
tool.