Reachability in Multi-Pushdown Automata

A research project under Prof. Mohamed Faouzi Atig at Uppsala Universitet and Prof. Krishna at IIT Bombay.

The project started off by an analysis of the methods presented in the following paper by Czerwinski et al: Reachability in MPDAs. First, I made a detailed report on why the problem is NP-Hard, by a reduction from the uniform word problem over commutative context free grammars (see this paper).

Following the established NP-Hardness, we examined the non-deterministic polynomial time algorithm for stateless strongly normed automata. First, we analyzed the case when the target configuration is comprised of empty stacks. For this special case, it is easy to provide a polynomial time reachability algorithm, along the lines of the CYK-algorithm for typical context free grammars. However, for the general target configuration, the non-deterministic algorithm is quite involved, since it is difficult to characterize the existence of a possibly exponential length path using only polynomial sized characterizations. However by marking the appropriately relevant transitions and tracking only the transitions that actually appear in the target, it becomes possible to provide a polynomial sized characterization, with the assumption of strong normedness. The problem of whether such a characterization exists for the unnormed cases remains open.

Next, we approached the problem from the other end, trying to establish hardness results for some of the open cases left by Czerwinski. In particular, the case where states are unrestricted, even with two stacks an MPDA can simulate a lossy FIFO systems, which are known to be atleast non-primitive recursive in hardness. Thus, the only decidable case for the unrestricted states case, is non-primitive recursive hard (yikes!)

For further work, a promising line seems to be via the establishment of two-player games with reachability objectives on the MPDA system. This will simulate adversarial conditions on concurrent systems modelled by MPDAs, and shed light on adversarial avoidability of race conditions.

A detailed report containing all the relevant resources and proofs will appear on this website shortly.

Symmetric Mixed Strategy Nash Equilibrium in n-Firm Location

It is well known that in the two player beach problem, there exists a unique nash equilibrium in mixed strategies, which is the pure strategy vector \((0.5,0.5)\). It is also well known that the 3-player version doesn't have any pure strategy nash equilibrium. However, there exists an interesting MSNE in the 3 player case. We restrict our analysis to symmetric equilibria, where every player uses the same mixed strategy and hence gets the same utility.

Why symmetric? When we look at the case with a larger number of firms, in particular with 5 firms, we see that the pure strategy equilibrium given by positions \(\dfrac{1}{6},\dfrac{1}{6}, \dfrac{1}{2}, \dfrac{5}{6}, \dfrac{5}{6}\) involves the middle player taking away the lion's share of customers. Thus, this equilibrium is not symmetric. One might consider a uniform choice of permutation among all players, but that leads to a correlated equilibrium. Naturally the question about an independent and symmetric mixed strategy equilibrium arises.

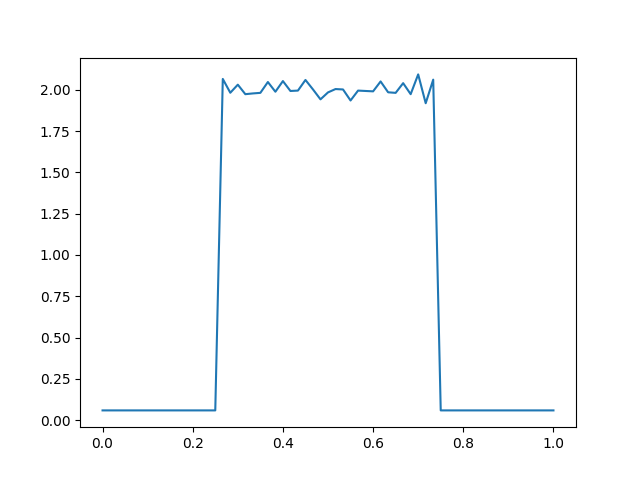
To answer this question, I resorted to the simple method of simulation, and gradient descent. We assume a probaility distribution, and slowly optimize it towards equilibrium using a simple gradient descent based approach. In essence, we look for a pure strategy that is beneficial to deviate to, and add probability mass to it. Further, for simulation the continuous game is reduced to the discrete version where the positions may be one of \(N\) uniform positions on the beach. By extending Nash's theorem, we can show the existence of a symmetric mixed strategy equilibrium in this scenario. We simply take the limit for a large number of divisions (\(100\) should suffice) to predict the symmetric MSNE. Here is a sample plot for 3 firms, that clearly demonstrates the MSNE being uniform over \(0.25, 0.75\) and \(0\) elsewhere.

Mentor for FAST-G

The idea behind FAST-G was to implement various optimization algorithms related to graphs that are often analyzed only in theory and left without implementation. In particular, we focused on optimization related to paths, trees, matchings and flows. The culmination of the project was LP-based matching algorithms that are the best combinatorially. In future work, we aim to investigate the recent breakthrough on the flow problem reducing it to linear time. The progress made by each mentee can be seen in the PRs of the linked repo.

Rendera

A coding project under the Summer of Code 2022, initiative of WnCC, IIT Bombay.

The project involved making a Ray-Tracing engine written in C++17, from scratch, including our very own math utilities. It was my first project and it helped me learn programming etiquette and familiarized me with object oriented programming. My contributions included the first render of a sphere under a point light source using the Phong Model of illumination, and writing a generalized lights class, aside from setting up robust math primitive utilities.

Combinatorial Game Theory

A learning project under the Summer of Science 2022, initiative of MnP Club, IIT Bombay.

I had started this project as a learning project on Game Theory, but I found Combinatorial Games more interesting. Taking the prototypical example of Red-Blue Hackenbush, the theory of partizan game values, and surreal numbers is discussed. I used Conway's amazing book On Numbers and Games, and Berlekamp, Conway and Guy's comprehensive textbook Winning Ways for your Mathematical Plays. The theory is quite rich and very complicated, and I am currently exploring it's computational side. The project is the chief inspiration and reference for my 2nd blogpost on OMC.

Mathematics and Physics Club

I am a convener for the Mathematics and Physics Club at IIT Bombay. Our aim is to create a collaborative and interactive community among math and physics enthusiasts in the institute. We conduct various fun events for this purpose. The Mathathon 2022, our very own math olympiad was held successfully on the 13th of August, 2022 with great participation, and was very fun.

Team SeDriCa - UMIC IITB

In early April 2022, I joined the Unmesh Mashruwala Innovation Cell- Team SeDriCa, a tech-team at IIT Bombay, working to build an autonomous self-driving car. I was recruited to join the Computer Vision subdivision, where I learnt various Image Processing Methods and Machine Learning models to assist with the Computer Vision component of the Self-Driving Car. Do make sure to check out their youtube series of videos explaining what we do and how!