 |
 |
Policy Iteration is a classical, widely-used family of algorithms to compute an optimal policy for a given Markov Decision Problem. This tutorial will present the few theoretical results that are currently known on the running-time of policy iteration—results that lie at the edge of a substantial gap in our knowledge.
 |

 |
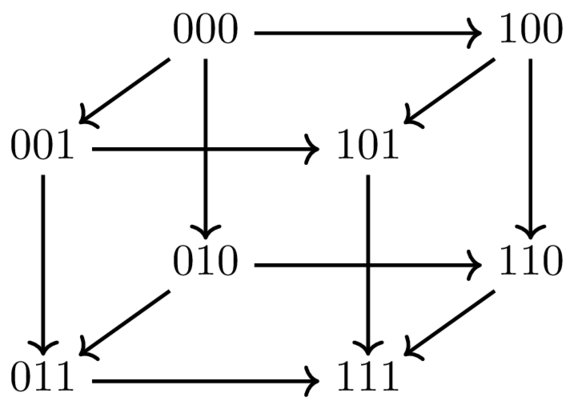
Markov Decision Problems (MDPs) are a well-studied abstraction of sequential decision making. Policy Iteration (PI) is a classical, widely-used family of algorithms to compute an optimal policy for a given MDP. PI is extremely efficient on MDPs typically encountered in practice. PI is also appealing from a theoretical standpoint, since it naturally yields "strong" running time bounds for MDP planning. Strong bounds depend only on the number of states and actions in the MDP, and not on additional parameters such as the discount factor and the size of the real-valued coefficients.
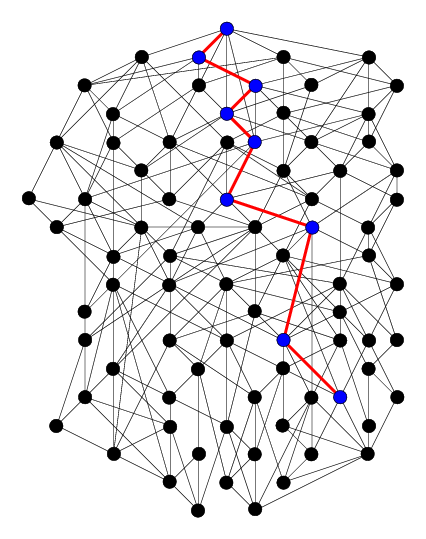
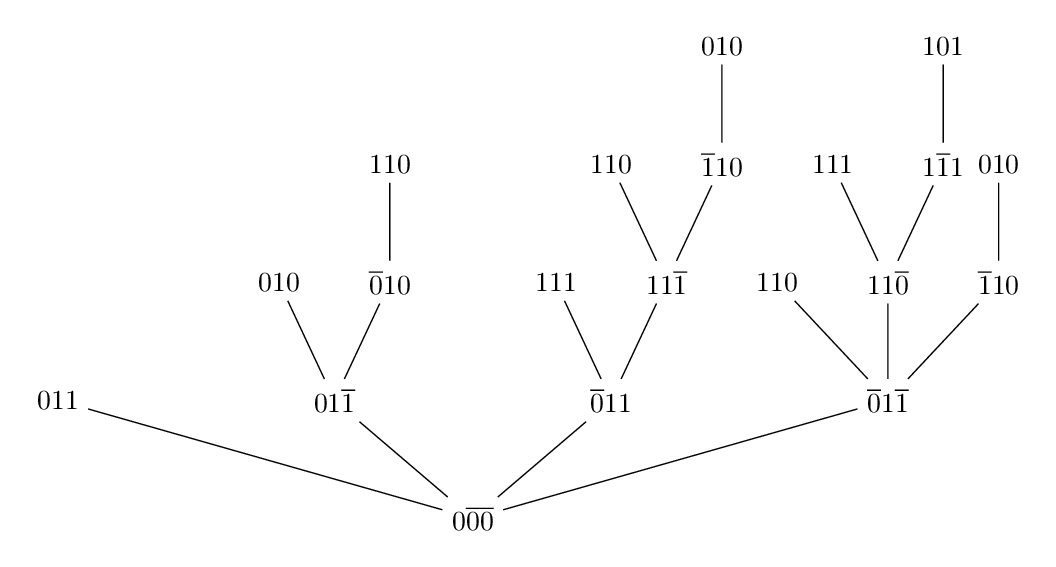
It has proven surprisingly difficult to establish tight theoretical upper bounds on the running time of PI. As a case in point, consider Howard's PI (Howard, 1960), the canonical variant of PI that was proposed over half a century ago. On MDPs with n states and 2 actions per state, the trivial upper bound on the number of iterations taken by this algorithm is 2n. It was not until 1999 that the trivial bound was improved, and that by a mere linear factor (to O(2n/n)) (Mansour and Singh, 1999). This upper bound remains the tightest known to date for Howard's PI. While we may be tempted to surmise that the algorithm could indeed be that slow, the tightest lower bound that has been proven is only Ω(n). Clearly, these results leave a yawning gap for theoretical analysis to fill.
The tightest upper bounds currently known for the PI family correspond to variants that are different from Howard's PI. These upper bounds—O(1.6479)n iterations for 2-action MDPs, and (2+ln(k-1))n iterations for k-action MDPs, k > 2—were obtained only in 2016. The new approaches that have yielded these recent improvements could possibly lead to even tighter bounds for Howard's PI, which experiments suggest remains the most effective variant in practice.
The PI algorithm is taught in basic courses on sequential decision making and reinforcement learning, and routinely used in deployed systems. However, subsequent to the paper by Mansour and Singh (1999), the AI community has not given much attention to the theoretical analysis of PI. Given how well we know the method itself, it is surprising how little we know about its theoretical properties.
The analysis of PI continues to attract interest from areas such as formal verification, algorithms, and operations research. In fact, some of the presenter's recent contributions to the problem (Kalyanakrishnan, Mall, and Goyal, 2016; Kalyanakrishnan, Misra, and Gopalan, 2016; Gupta and Kalyanakrishnan, 2017) build upon ideas developed in these affiliate fields. This tutorial aims to reinvigorate the AI community—experts and novices alike—to pursue theoretical research on PI.
The tutorial will introduce the audience to the PI family of algorithms, describe tools for analysis, present corresponding theoretical results, and highlight open problems for future research. A detailed outline is provided below.
The tutorial will be accessible to anyone with a background in computer science, since the analysis of PI mainly involves techniques such as counting and logical reasoning about discrete structures. The tutorial will build upon basic results such as the existence of optimal policies and the proof of the policy improvement theorem. Although no knowledge of existing results is assumed, those already familiar with MDPs and sequential decision making are likely to benefit the most.