Description

We are all familiar with the traditional notion of theorem and proof (i.e., as taught in CS208). In this course we will explore what it means to relax this notion to "probabilistic" proofs, where soundness is required to hold with a high-enough probability. In particular, we will cover:

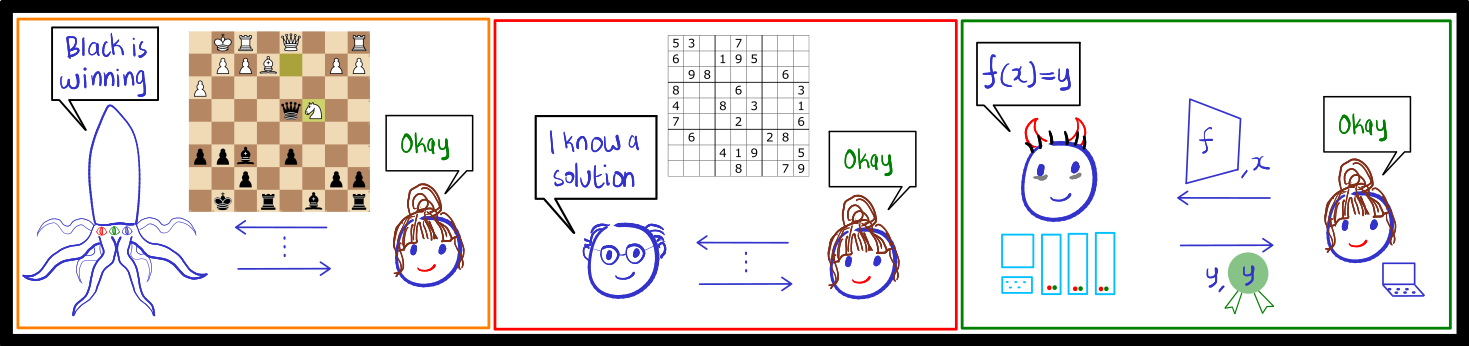
• Interactive proofs which, e.g., allows an efficient verifier, Vera, to verify that a certain chess position is winning for black
• Probabilistically-checkable proofs, which allows Vera to verify that a theorem is true while having to check only a small part of the proof
• Zero-knowledge proofs which, e.g., allows Vera to verify that Peter (the prover) knows a solution to a Sudoku puzzle while learning no additional information about the solution
• SNARGs which, e.g., allows Vera to verify that a resource-intensive computation she delegated to the cloud has been correctly executed

These proofs have turned out to have far-reaching theoretical consequences to complexity theory and cryptography. And more recently, such relaxed notions of proof systems have also been found to be extremely useful in practice, with applications ranging from blockchains (examples 1 and 2) to cloud computing. In this course, we will study such proof systems in depth, mainly from a theoretical perspective, but motivated by real-world applications.

Prerequisites

Discrete structures and probability theory will be assumed. Basic knowledge of basic cryptography and complexity theory is a plus, but I will reintroduce the necessary notions whenever needed. The course will have a theoretical flavour, and thus we will expect some mathematical maturity.

Who can credit?

The course is open to (all PGs) and (UGs in third and fourth years).

Grading and Attendance

Weightage	Towards
30%	End-sem
25%	Mid-sem
20%	Paper presentation (two students per paper)
15%	Three graded assignments
5%	Class participation
5%	Scribing (~2 lectures per student)

• Attendance is not mandatory (but encouraged)
• You are free to collaborate/discuss while solving assignments (list your collaborators in your submission), but you must write up your own solution.
• Please use this \(\LaTeX\) template for scribing -- you will find the necessary instructions in the \(\LaTeX\) file. In case you have trouble compiling, drop by my office.

---

#	Date	Notes	Details
L1	06/Jan	[↗]	Topics covered Administrivia Overview of the course Probabilistically checking matrix multiplication: Freivalds' algorithm
Module I: Interactive Proof (IP)
L2	09/Jan	[↗]	Topics covered Another look at Freivalds' algorithm Finite fields and polynomials over finite fields Main tool: Schwartz-Zippel Lemma
L3	13/Jan		Topics covered (IP I) Definining Interactive Protocols IP for Graph Non-Isomorphism (GNI)
L4	16/Jan		Topics covered (IP II) Reducing errors by repetition Main tool: Chernoff Bound
L5	20/Jan		Topics covered (IP III) Sumcheck protocol: interactive protocol for \(\#\)SAT Main tool: arithmetisation
L6	23/Jan		Topics covered (IP IV) \(\mathbf{IP}=\mathbf{PSPACE}\) Interactive protocol for TQBF Main tool: linearisation
A1	20/Jan	[↗]	Assignment 1
L7	27/Jan		Topics covered (IP VI) Public-coin vs private coin Set lower-bound protocol Main tool: approximate counting using pairwise-independent hashing
Module II: Zero-Knowledge (ZK) and Probabilistically-Checkable Proof (PCP)
L8	30/Jan		Topics covered (ZK I) Defining zero-knowledge: the simulation paradigm Honest-verifier perfect ZK-IP for Graph Isomorphism (GI) and GNI Malicious-verifier perfect ZK-IP for GI
L9	03/Feb		Topics covered (ZK II) Limitations of Perfect ZK Relaxing to statistical ZK: statistical distance, statistical indistinguishability Class \(\mathbf{SZK}\) Statistical ZKP for "Statistical Closeness" problem
L10	06/Feb		Topics covered (ZK III) Polarisation of distributions A complete problem for \(\mathbf{SZK}\) Other properties of \(\mathbf{SZK}\)
L11	10/Feb		Topics covered (PCP I) The PCP model A simple exponentially-long PCP for GNI Basics of error correcting codes
L12	13/Feb		Topics covered (PCP II) Walsh-Hadamard (WH) code Main tools: linearity testing and local decoding
A2	14/Feb	[↗]	Assignment 2
L13	17/Feb		Topics covered (PCP III) LE-SAT and QE-SAT: satisfiablility of system of linear and quadratic equations Warm-up: exponentially-long PCP for LE-SAT Exponentially-long PCP for QE-SAT Main tool: quadratic test
L14	20/Feb		Topics covered (PCP IV) Reed-Muller code Polynomially-long PCP for QE-SAT Main tool: low-degree extensions and sumcheck
M	28/Feb	[↗]	Mid-sem: 14:30-16:30 in CC105
Module III: Cryptographic Proof Systems
L15	03/Mar		Topics covered (Succinct Argument I) Impossibility of succinct (interactive) proof IP Basic cryptography: PPT adversaries and hardness assumptions Collision-resistant hash function
L16	06/Mar		Topics covered (Succinct Argument II) Succinct (interactive) argument Succinct argument for \(\mathbf{NP}\) from PCPs: Kilian's Protocol Merkle hash and local opening
SQ2	06/Mar		Crib session for Mid-sem
L17	10/Mar		Topics covered (SNARG I) Succinct non-interactive argument (SNARG) Random-oracle model (ROM) and Fiat-Shamir Transform (FST) SNARG for \(\mathbf{NP}\) in ROM
A1	10/Mar	[↗]	Assignment 3
L18	13/Mar		Topics covered (SNARG II) FST continued Soundness of FST for multi-round protocols Round-by-round soundness
L19	17/Mar		Topics covered (ZK IV) Computational ZK proof Computational ZK proof for Graph Hamiltonicity: Blum's Protocol
L20	20/Mar		Topics covered (ZK V) Commitment Schemes Statistically-binding commitment from pseudo-random generators: Naor's commitment Statistically-hiding commitment and SZK arguments
L21	24/Mar		Topics covered (NIZK I) Non-interactive Zero-knowledge (NIZK) Common reference string (CRS) and hidden bit (HBM) models One-way permutation and hard-core predicates CRS-NIZK from HBM-NIZK
L22	27/Mar		Topics covered (NIZK II) HBM-NIZK for Graph Hamiltonicity
H	31/Mar		No lecture (Id-ul-Fitr)
Module IV: Paper presentations
L23	03/Apr		Paper I Title: Multi-prover interactive proofs: how to remove intractability assumptions Presenters: Kalvala Vivek and Krishna Narasimhan Agaram
L24	07/Apr		Paper II Title: Fast Reed-Solomon Interactive Oracle Proofs of Proximity Presenters: Nilabha Saha and Lakshya Gadhwal
H	10/Apr		No lecture (Mahavir Jayanti)
L25	14/Apr		Paper III Title: Perfect Zero-Knowledge PCPs for \(\#\mathbf{P}\) Presenters: Samipa Samanta and Ravi Prakash
L26	17/Apr		Paper IV Title: Finding a Nash Equilibrium Is No Easier Than Breaking Fiat-Shamir Presenters: Priyanshu Singh and Kunal Chaudhari
E	29/Apr	[↗]	End-Sem: 18:00-21:00 in CC105

---

Below you can find the list of resources relevant to this course. The resources (e.g., further reading) for a particular lecture can be found in the lecture notes.

Textbooks and Monographs

• Computational Complexity: A Modern Approach, by Sanjeev Arora and Boaz Barak.
• Foundations of Cryptography, Volume I by Oded Goldreich
• Proofs, Arguments, and Zero-Knowledge, by Justin Thaler
• Building Cryptographic Proofs from Hash Functions, by Alessandro Chiesa and Eylon Yogev

Related Courses

• Foundations of Probabilistic Proofs (CS294, Fall 202) by Alessandro Chiesa
• Foundations and Frontiers of Probabilistic Proofs (Virtual School) by Alessandro Chiesa and Tom Gur
• Probabilistic Proof Systems by Prashant Nalini Vasudevan
• Advanced Topics in Cryptography: Cryptographic Proofs (6.876, Fall 2019) by Alex Lombardi
• Proof Systems in Cryptography (E0314, Spring 2021) by Chaya Ganesh

Background Material

• The relevant mathematical background required for this course can be found in Appendix A of Arora-Barak
• Basic computational complexity can be found in the second recitation of MIT6875.