CAPSDoc

Table of Contents

1 What is CAPS?

CAPS is a system for the derivation of imperative programs from formal specifications. The system provides a tactic based framework for carrying out program as well as formula transformations in a coherent way. It automates the mundane formula manipulation tasks by employing automated theorem provers.

2 Derivation Methodology

While developing program in CAPS, at every stage, there is always a correct-by-construction partial program with some unknown subprograms, as shown in the example in Figure 1.

Max SegSum Example image

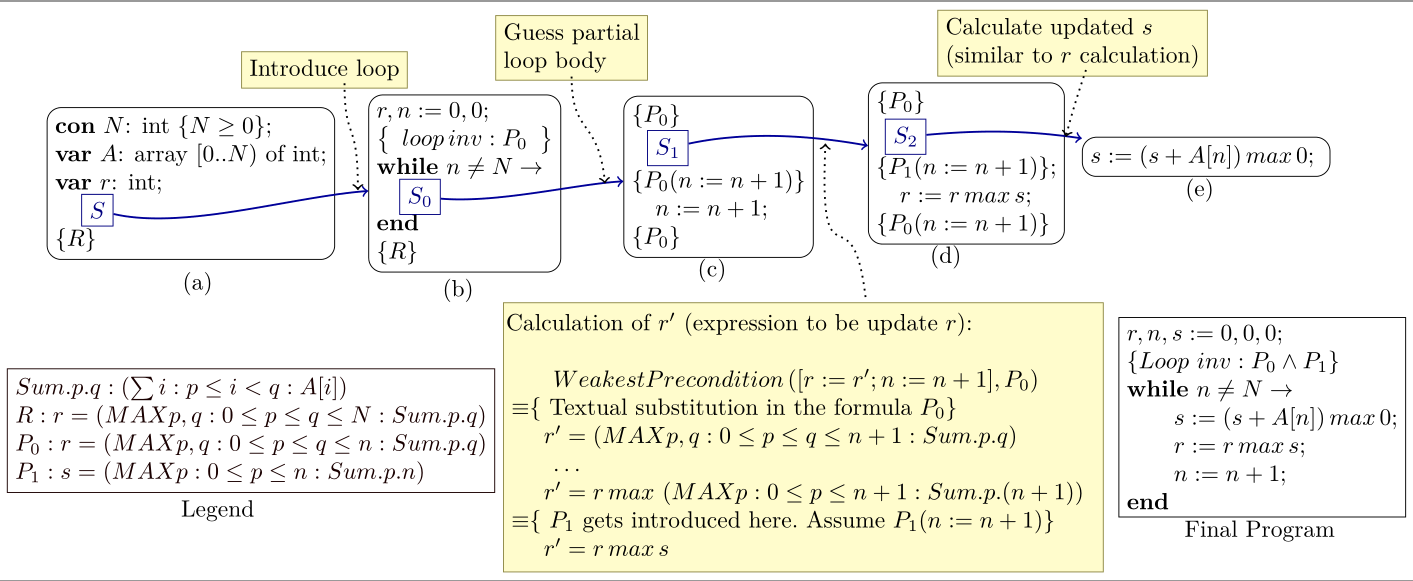
Figure 1: Sketch of an example derivation (maximum segment sum problem)

All program constructs in the system, including the unknown subprograms have associated pre- and post-conditions. Program constructs are introduced only when logical manipulations show them to be sufficient for maintaining the correctness. For example, in Figure 1(c), variable \(r\) needs to be modified in the loop body to maintain the loop invariant \(P_0\) . The required update for \(r\) naturally follows from the simplification of the correctness proof obligations. An important feature of our system is that a user cannot construct an incorrect program in it. Apart from the fully annotated derived program, the system also maintains the derivation tree which reproduces the complete derivation process and provides opportunities for exploring the alternative solutions by backtracking and branching.

3 Related Publications

Theoretical foundations

System building aspect

Educational Usage

4 Installation

4.1 Prerequisites

4.1.1 System Requirements

  • Linux
  • Google Chrome Browser

4.1.2 Prerequisites

  • Java Runtime Environment
  • Why3 verification framework (v0.81)

    As a part of the Why3 installation, you will also need to install the external provers. Following external provers are supported in CAPS.

    • Z3
    • Alt-Ergo
    • CVC3
    • SPASS

At least one of these theorem provers needs to be installed. We recommend Z3 since CAPS can also connect to Z3 directly.

4.1.3 Why3 Installation

The following instructions should work. In case of problems, please refer detailed installation instructions at the Why3 homepage (http://why3.lri.fr/).

  1. Install Ocaml and libraries

    http://why3.lri.fr/doc-0.81/manual006.html#sec38 

    sudo apt-get install ocaml ocaml-native-compilers
sudo apt-get install liblablgtk2-ocaml-dev liblablgtksourceview2-ocaml-dev libocamlgraph-ocaml-dev
  2. Install Why3
    wget https://gforge.inria.fr/frs/download.php/file/33491/why3-0.81.tar.gz
tar -xzf why3-0.81.tar.gz
cd why3-0.81/
./configure

    Make sure that the "configure" is successful. Sample configure summary below. 

                     Summary
-----------------------------------------
Verbose make            : no
OCaml compiler          : yes
    Version             : 3.12.1
    Library path        : /usr/lib/ocaml
    Native compilation  : yes
    Profiling           : no
IDE                     : yes
Bench tool              : no
Documentation           : no
Coq support             : no (coqc not found)
PVS support             : no (pvs not found)
Frama-C support         : no
Hypothesis selection    : yes
Installable             : yes
    Binary path         : ${exec_prefix}/bin
    Data path           : ${prefix}/share/why3
    Relocatable         : no

    Proceed with the installation. 

    make
sudo make install
cd ..

4.1.4 Z3 Installation

Download Z3 v4.3.1 source: Z3 v4.3.1 Source 

sudo apt-get install python autoconf
unzip z3-89c1785b73225a1b363c0e485f854613121b70a7.zip -d z3
cd z3
autoconf
./configure
python scripts/mk_make.py
cd build
make
sudo make install

4.1.5 Configure Why3 to detect provers

Run the following command to to detect freshly installed provers. 

why3config --detect-provers

4.2 CAPS Installation

The latest version of the CAPS can be downloaded here.

Extract the archive. It contains the following files. 

application.conf            # Sample config file
staged/
start                       # start script

Update the Why3 path and other variables in the application.conf file.

Run the start command to start the server 

chmod u+x ./start
./start -Dconfig.file=./application.conf

Connect to http://localhost:9000 to access the CAPS application GUI. Login with user name user1@company.com and passsword secret1.

5 Usage

(The videos are for the older version. The tactic names and parameters might not match.)

5.1 Starting the derivation

Start the derivation by applying the `Init4` tactic.

5.2 Steps for deriving "If" program constructs

There two ways of deriving if program construct

5.2.1 IfIntro

You can directly introduce an If program construct by directly providing the guards of the If Program (IfIntro tactic).

5.2.2 StepIntoBA and StepIntoIFBA

  • Start the derivation by applying the StepIntoBA tactic on an UnknownProgram node. You will need to specify the variables that occur on the left hand side of the assignments in the body of the if. For example, if there are three variables x, y, and z but you don't intend to make any assignment to z, then can you can just specify variables x and y
  • Once in the formula mode, you can instantiate meta variables by applying the InstantiateMeta tactic and guess the guards by applying the GuessGuard tactic. On stepping out from the formula mode, an IfProgram is constructed form the guessed guards and instantiated meta variables.
  • To derive additional guards, apply the StepIntoIFBA tactic to the IF program.

5.3 Propagating Assumptions

5.4 Stepping into subprograms

To step into a subformula, apply the `StepIntoProgId` tactic.

5.5 Stepping into subformulas

To step into a subformula, apply the `StepIntoSubFormula` tactic.

5.6 SimplifyAuto tactic

To simplify the current formula with the help of ATPS, apply `SimplifyAuto` tactic.

5.7 Input commands for logical operators

|-----------------------+---------------|
| operator              | Input command |
|-----------------------+---------------|
| Conjunction           | \and          |
| Disjunction           | \or           |
| Negation              | \neg          |
| Equivalence           | \equiv        |
| Implication           | \implies      |
| Universal Quantifier  | \forall       |
| Existential Quantifer | \exists       |
|-----------------------+---------------|

5.8 Input commands for arithmetic operators

|----------------+---------------|
| operator       | Input command |
|----------------+---------------|
| Addition       | +             |
| Subtraction    | -             |
| Multiplication | \ast          |
| Division       | \slash        |
|----------------+---------------|

6 Troubleshooting

6.1 I am getting TacticInputParseError(Failed to parse the tactic) error

  • Formulas like 0 ≤ i < N are not supported. Type them as 0 ≤ i \and i < N
  • Ensure that you have specified type for all the variables

6.2 IntroAssignmentTactic fails : Proof obligation for the assignment can not be discharged

  • Ensure that the external theorem provers are configured properly.

7 Source

Source is available at https://github.com/dipakc/CAPS

Derivation examples: DerivationExamples